Analytická geometrie

Analytická geometrie nám dovoluje zapsat geometrické problémy algebraicky a vyřešit je pomocí rovnic.

Nejjednodušší objekty popsatelné analyticky jsou body, úsečky a vektory v rovině nebo v prostoru. Když už umíme manipulovat s vektory, můžeme je použít například k popisu přímky nebo roviny.

V případě přímek a rovin se pořád ještě jedná o objekty popsatelné lineárními rovnicemi nebo soustavami lineárních rovnic. Pokud se začneme zabývat i kvadratickými rovnicemi, dokážeme popsat i kuželosečky v rovině, například kružnici, elipsu, parabolu a hyperbolu.

Dva významné typy problémů, které řešíme v rámci analytické geometrie jsou polohové úlohy, ve kterých vyšetřujeme vzájemnou polohu geometrických objektů, a metrické úlohy, ve kterých počítáme konkrétní číselnou hodnotu výsledku, jako je např. vzdálenost dvou bodů nebo úhel svíraný dvěma protínajícími se přímkami.

Body

Uvažujeme‑li body v rovině nebo v prostoru, kde máme zavedenou kartézskou soustavu souřadnic (v rovině se dvěma osami x, y nebo v prostoru se třemi osami x, y, z), můžeme body popsat číselně souřadnicemi v rovině, případně souřadnicemi v prostoru.

Pomocí souřadnic pak umíme spočítat vzdálenost dvou bodů „vzdušnou čarou“ – délku úsečky v rovině, případně v prostoru.

Souřadnice bodů v rovině

Souřadnice bodů většinou zapisujeme pomocí kartézské soustavy souřadnic v rovině, která má jako osy dvě kolmé přímky. Vodorovná přímka se tradičně označuje x a souřadnice podél této osy se zapisuje první. Svislá přímka se tradičně označuje y a souřadnice podle této osy se zapisuje druhá. Přímky x, y se protínají v bodě [0; 0].

Přímky x a y jsou souřadné osy, bod [0; 0] je počátek soustavy souřadnic.

Souřadnice bodů v prostoru

Kartézská soustava souřadnic v rovině je daná trojicí navzájem kolmých číselných os x, y, z, které se protínají v bodě [0; 0; 0].

Přímky x, y, z jsou souřadné osy v prostoru, bod [0; 0; 0] je počátek soustavy souřadnic

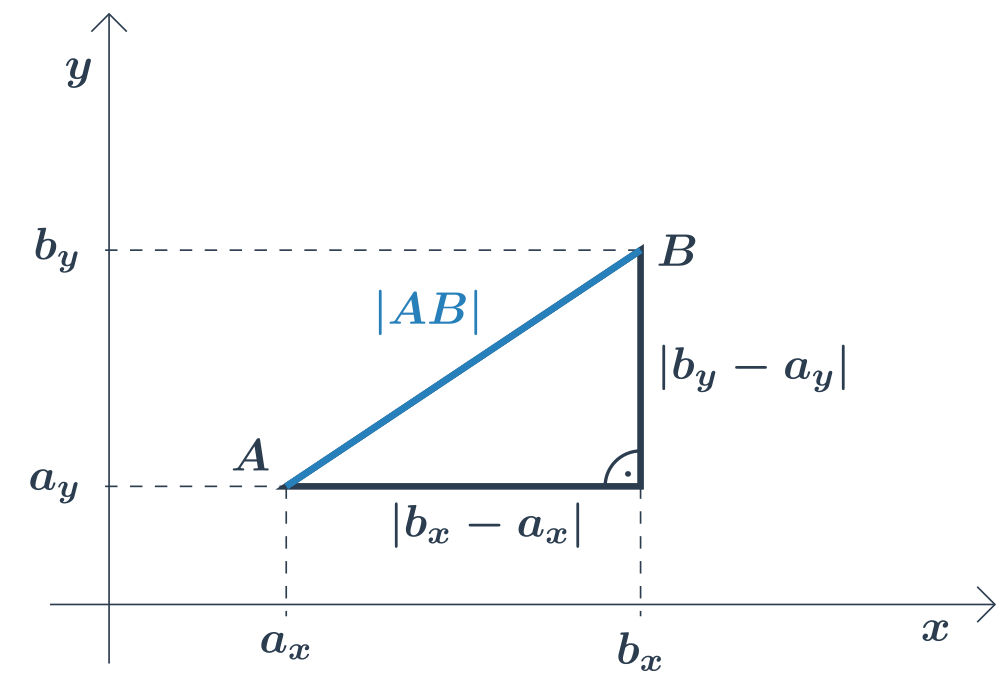
Vzdálenost bodů v rovině

Vzdálenost dvou bodů v rovině můžeme spočítat, když známe jejich souřadnice.

Jsou‑li dány souřadnice A = [ax, ay], B = [bx, by], je vzdálenost bodu A od bodu B:

|AB| = √(bx - ax)² + (by - ay)²

Vzoreček vychází z Pythagorovy věty. Všimněme si pravoúhlého trojúhelníku s délkami odvěsen (bx - ax) a (by - ay), jehož přepona má délku |AB|.

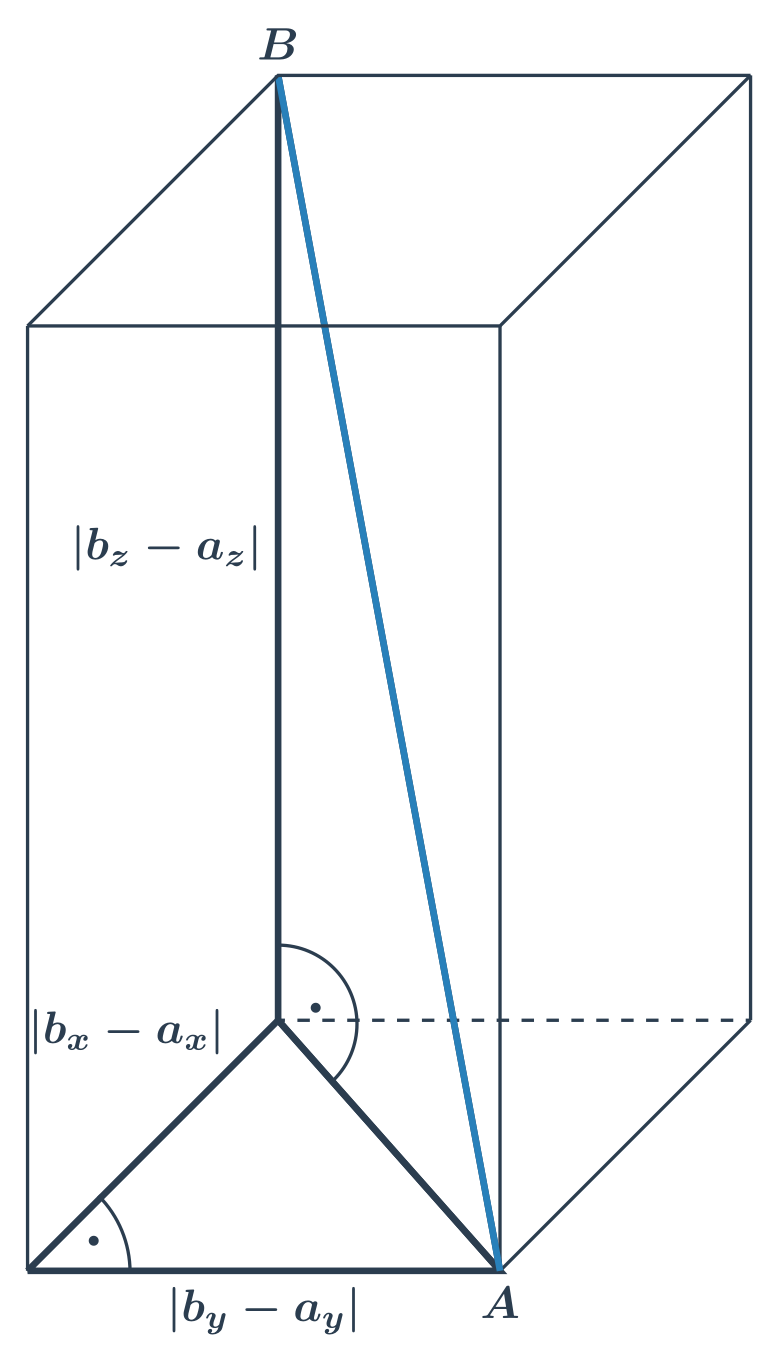
Vzdálenost bodů v prostoru

Vzdálenost dvou bodů v prostoru spočítáme podobně jako v rovině pomocí jejich souřadnic. Máme‑li souřadnice bodů A = (ax, ay, az), B = (by, by, bz), můžeme jejich vzdálenost určit takto:

|AB| = √(bx - ax)² + (by - ay)² + (bz - az)²

Úsečky

Úsečka je část přímky mezi dvěma krajními body (včetně těchto bodů). Úsečka je v rovině i v prostoru jednoznačně zadaná svými krajními body.

Délka úsečky v rovině

Délku úsečky v rovině spočítáme stejně jako vzdálenost bodů v rovině.

Jsou‑li dány souřadnice A[χA;χA]², B[χB;χB]², je délka úsečky AB

Vzoreček vychází z Pythagorovy věty.

Střed úsečky v rovině

Střed úsečky dělí úsečku na dvě stejné části. Pokud leží krajní body úsečky AB na číselné ose a jejich polohám odpovídají hodnoty α a b, potom jejímu středu S, odpovídá číslo s = a+b/2. Střed úsečky je „průměrem“ jejích krajních bodů.

Pro úsečku v rovině bude situace následující.

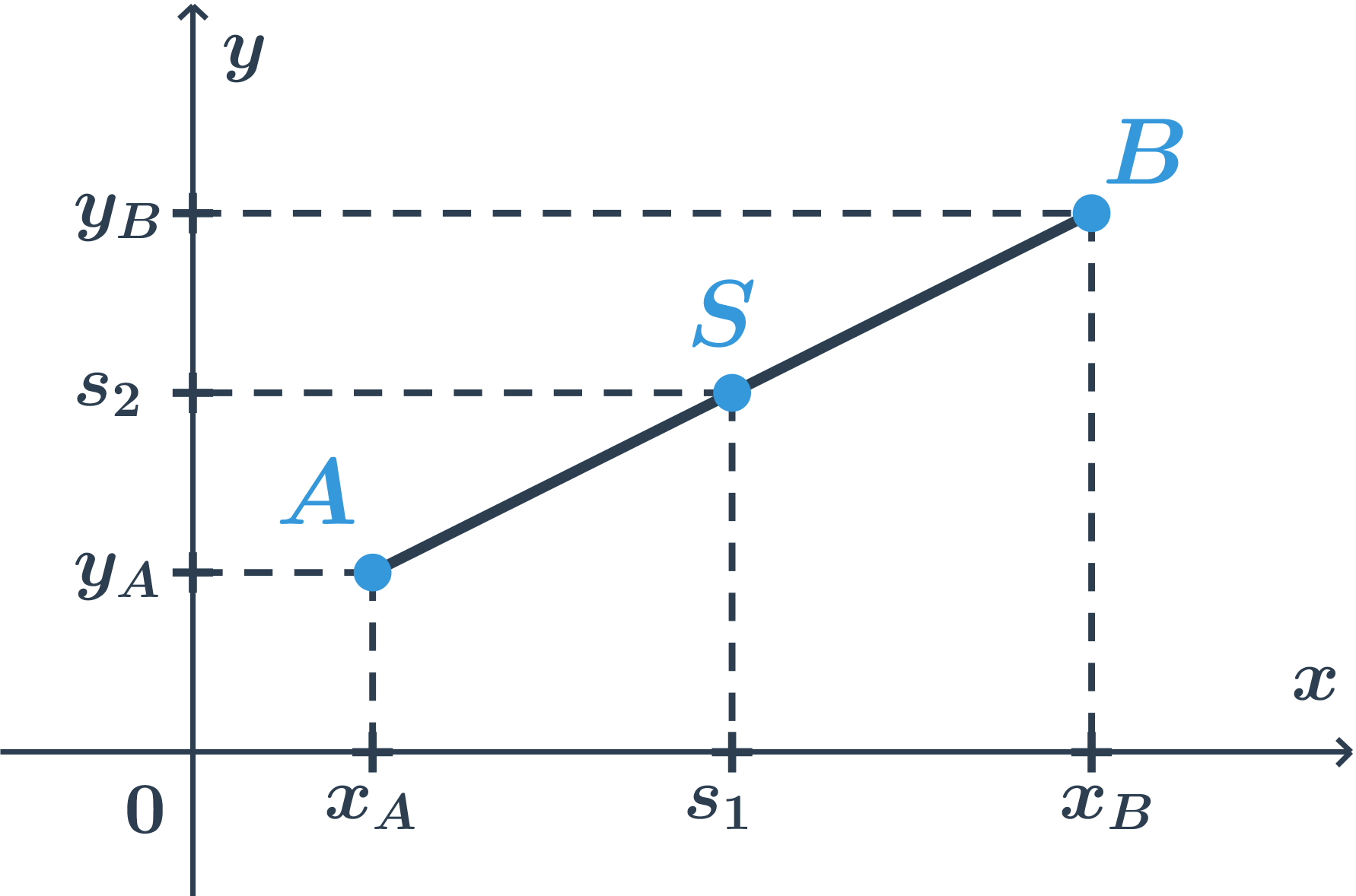
Situace na obou souřadných osách je stejná jako předtím. Spočítáme obě souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.

Pro střed S[s₁ + s₂] úsečky AB, kde A[xₐ;yₐ], E[xₑ;yₑ] platí:

s₁ = xₐ+xₑ/2, s₂ = yₐ+yₑ/2

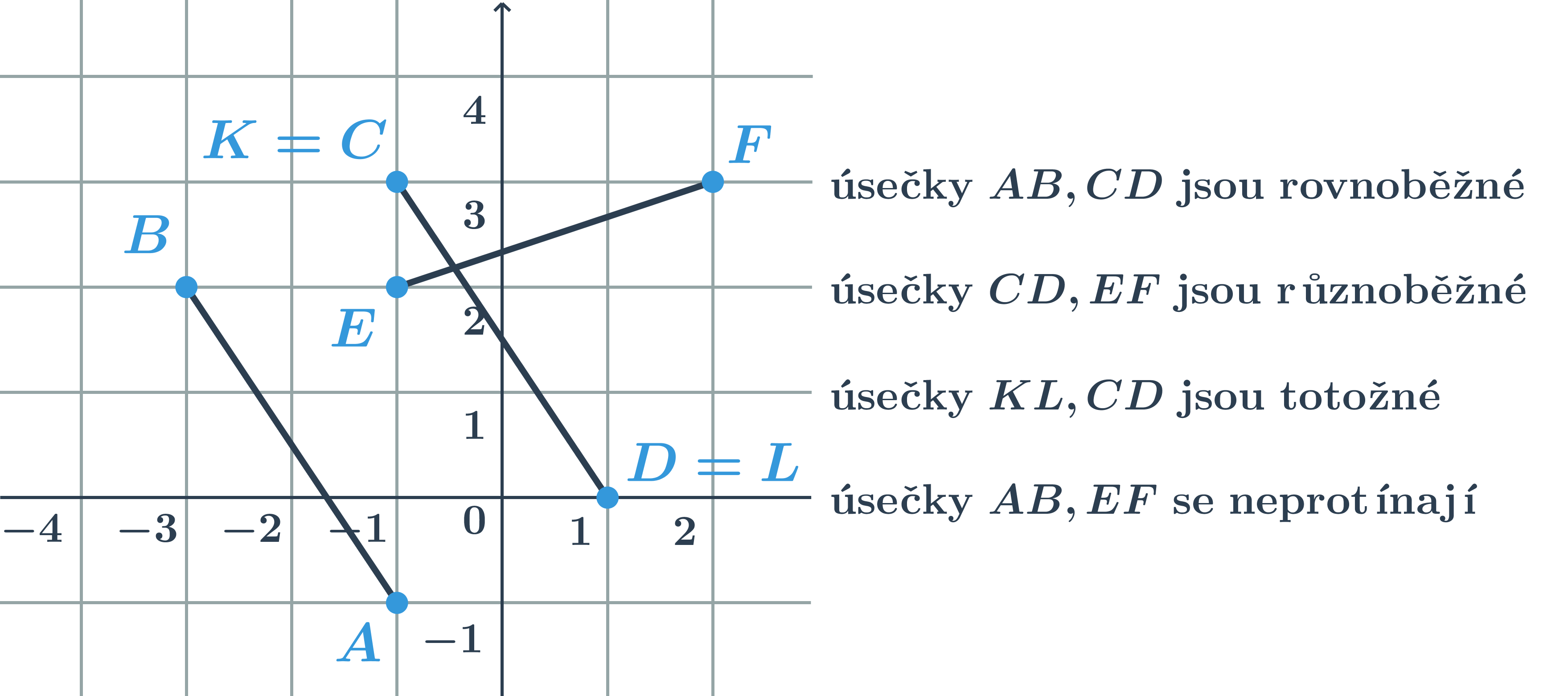
Vzájemná poloha úseček v rovině

Dvě úsečky v rovině mohou mít společné krajní body, pak říkáme, že jsou Totožně. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou ruznoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.

Délka úsečky v prostoru

Délku úsečky v prostoru spočítáme stejně jako vzdálenost bodů v prostoru.

Jsou‑li dány souřadnice A[xₓ;yₓ;zₓ], E[xₑ;yₑ;zₑ], je delka úsečky AB.

∣AB∣ = √(xₑxₓ)² + (yₑ + yₓ)² + (zₑ + zₓ)²

Střed úsečky v prostoru

Střed úsečky v prostoru spočítáme podobně jako střed úsečky v rovině. Spočítáme všechny souřadnice středu jako průměry odpovídajících souřadnic krajních bodů.

Pro střed S=(s₁;s₂;s₃) úsečky AB, kde A(xₐ;yₐ;zₐ), E(xₑ;yₑ;zₑ) platí:

s₁ = xₐ + xₑ/2, s₂ = yₐ + yₑ/2, s₃ = zₐ + zₑ/2

Vzájemná poloha úseček v prostoru

Podobně jako v rovině mohou mít dvě úsečky společné krajní body, pak říkáme, že jsou Totožné. Pokud se úsečky protínají v jednom bodě, říkáme, že jsou různoběžné. Úsečky se také nemusí protínat, nemají tedy žádný společný bod. Speciálně mohou v tomto případě být rovnoběžné.

Tyto vzájemné polohy si dobře můžeme ilustrovat na krychli.

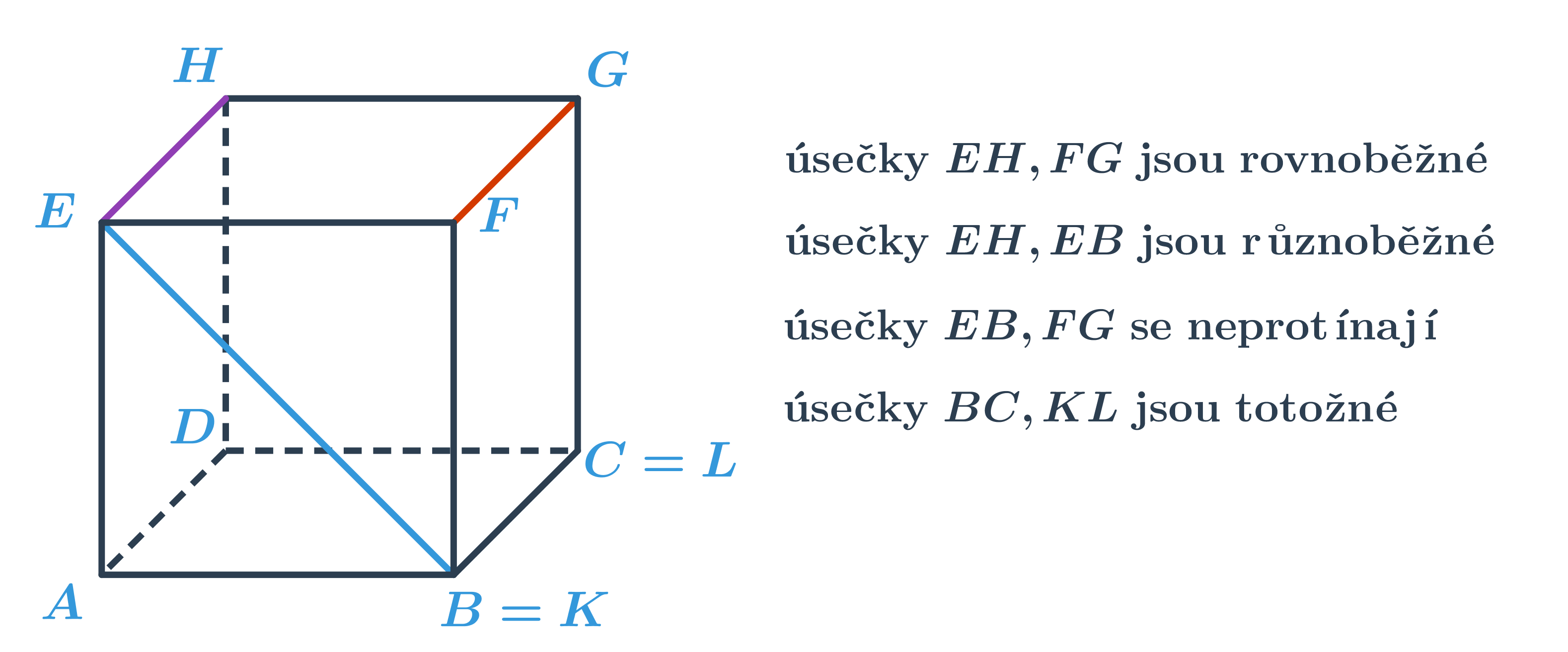
Vektory

Vektor je množina všech shodně orientovaných úseček, které mají stejnou délku. Každou z těchto úseček nazýváme umístěním vektoru.

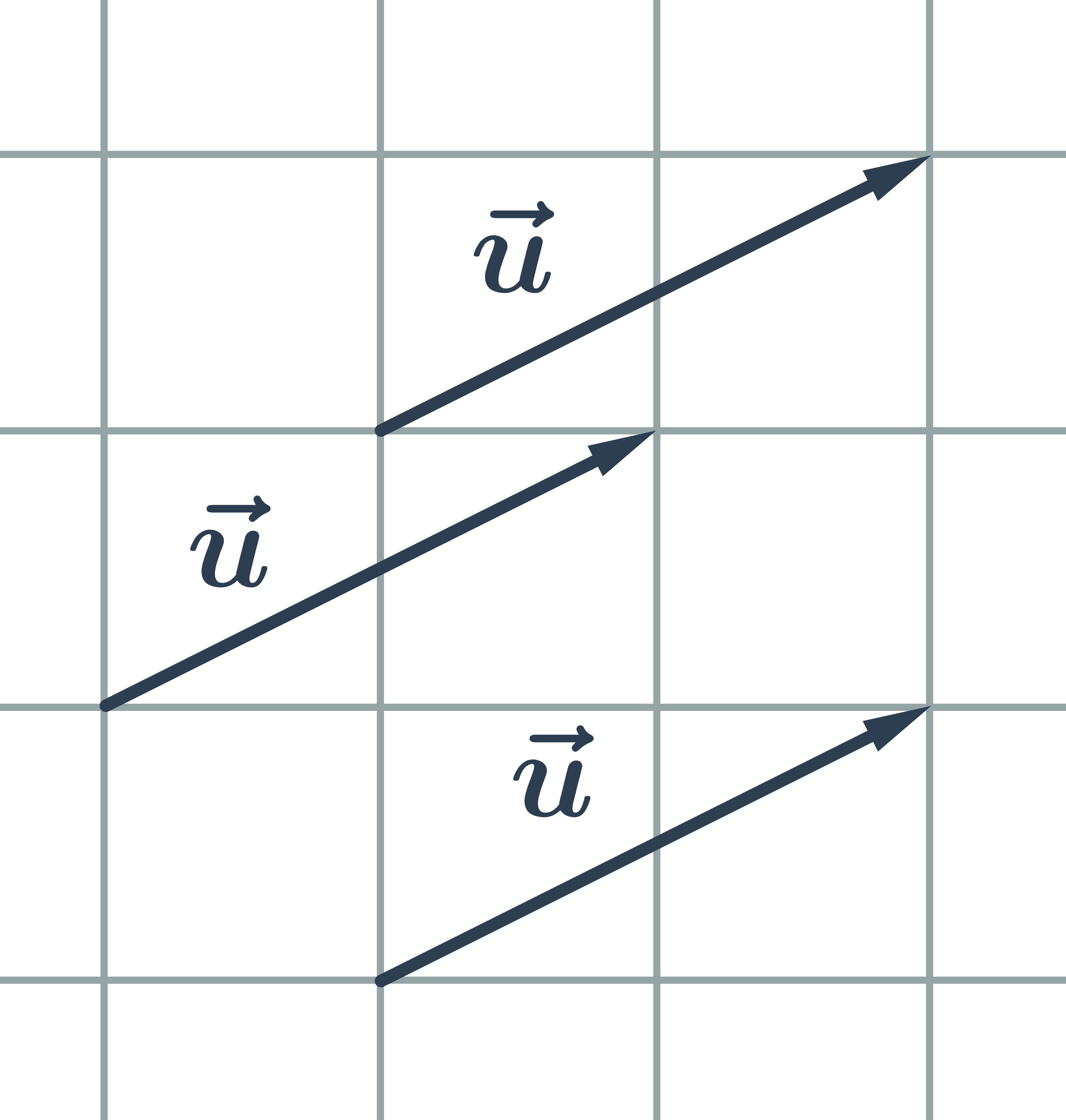
Vektory: pojmy

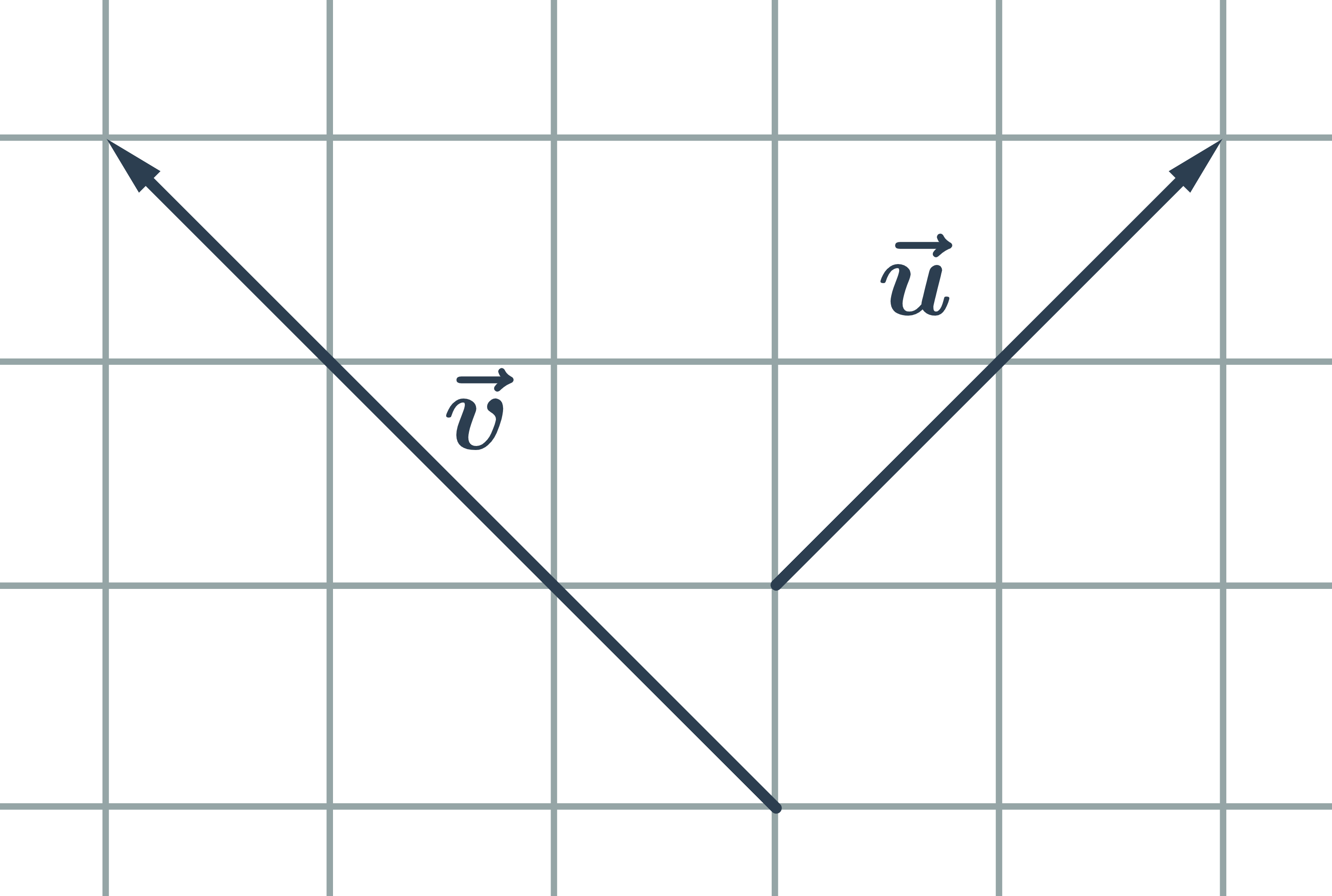
Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci:

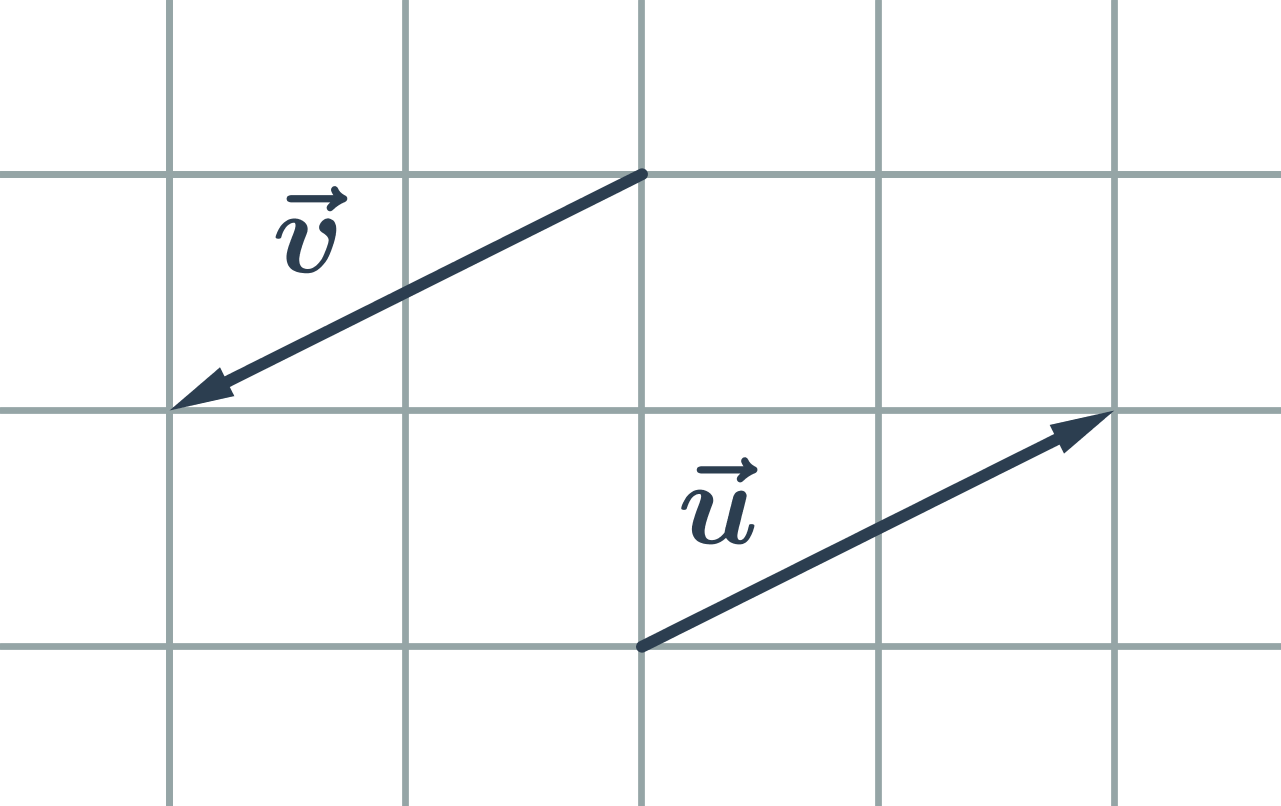
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. Tedy nemusí mít stejnou délku, mohou mít stejnou nebo opačnou orientaci:

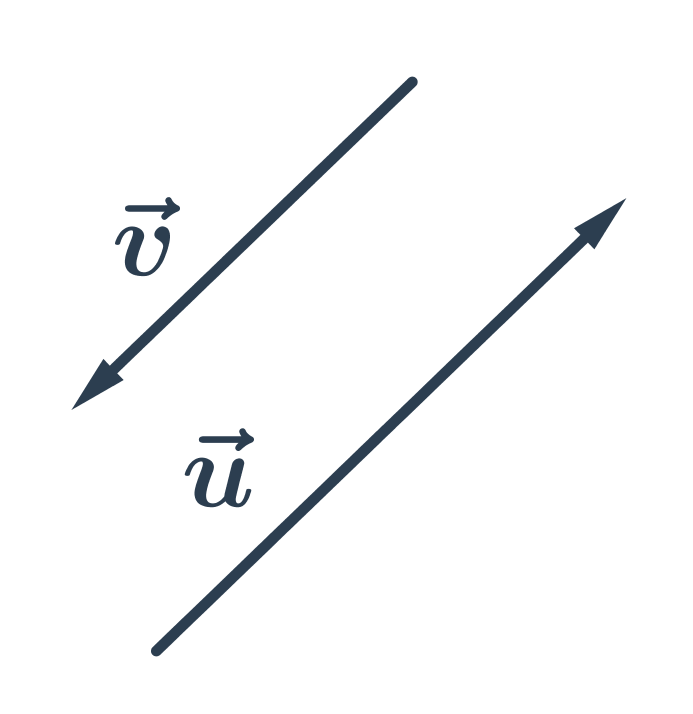
Kolmé vektory jsou vektory, které svírají pravý úhel:

Jednotkový vektor má delku 1.

Nulový vektor má nulovou délku, tedy splývá jeho počáteční a koncový bod.

Souřadnice vektoru

Již víme, že vektor je množina nekonečně mnoha orientovaných úseček, jedna z nich má počátek v počátku souřadného systému, v bodě ₒ = [0; 0]. Souřadnice koncového bodu jsou souřadnice daného vektoru.

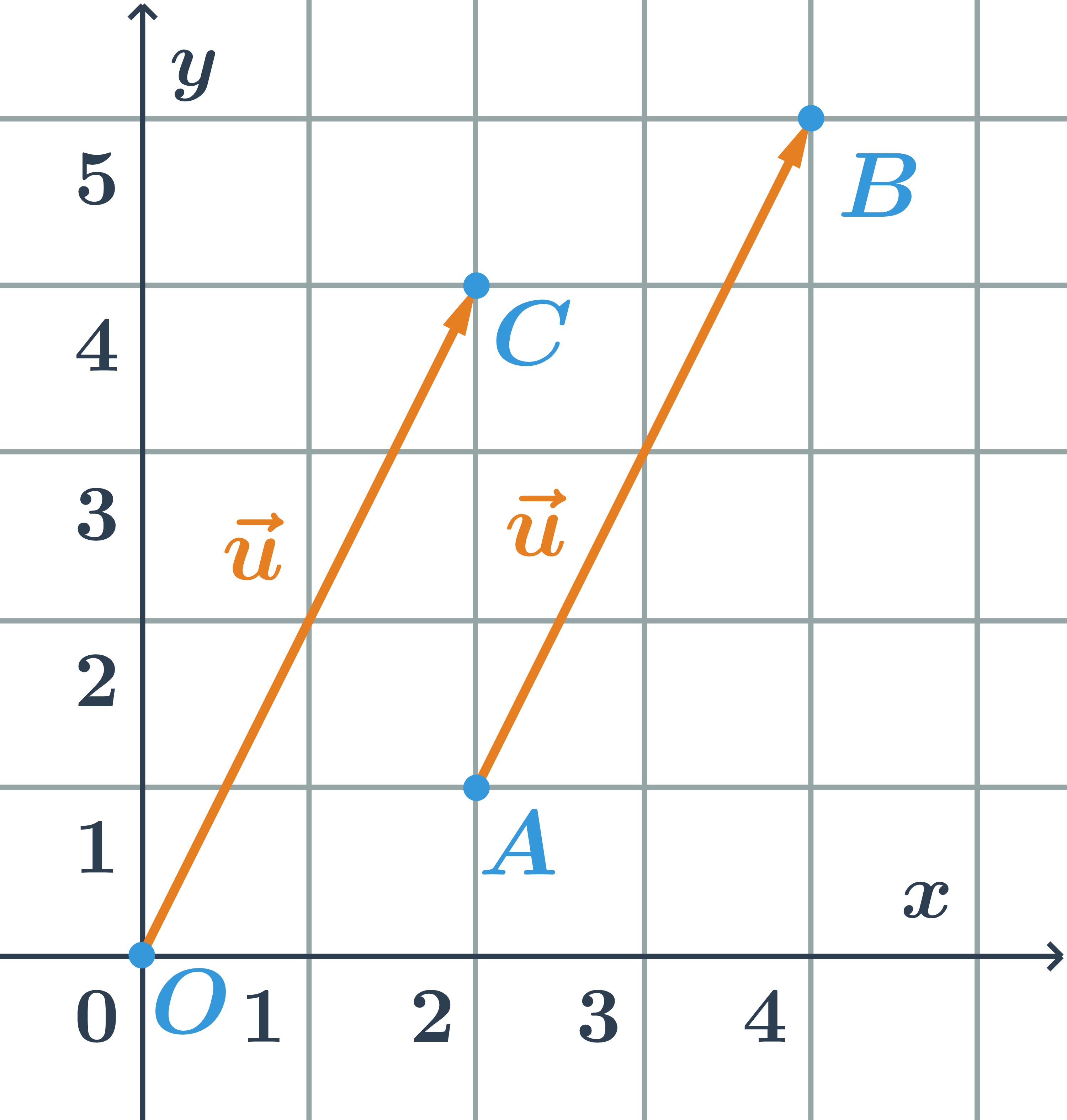
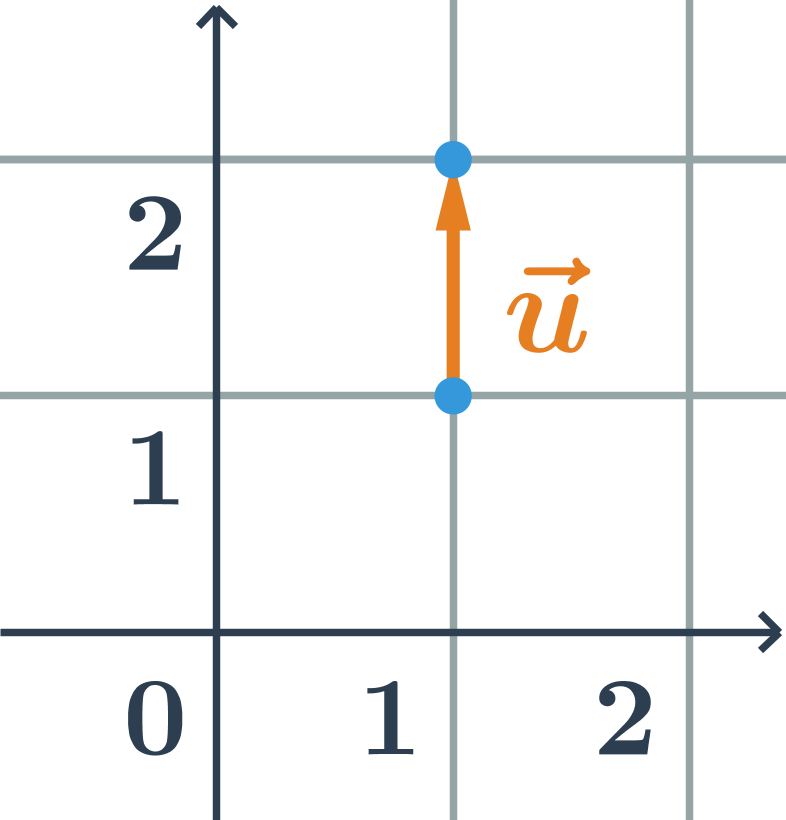
Velikost vektoru $\vec{AB}$ je délka úsečky AB. Vektor, který má délku 1, se nazývá jednotkový vektor:

Vektor, který má nulovou délku (počáteční a koncový bod vektoru splývá) se nazývá nulový vektor:

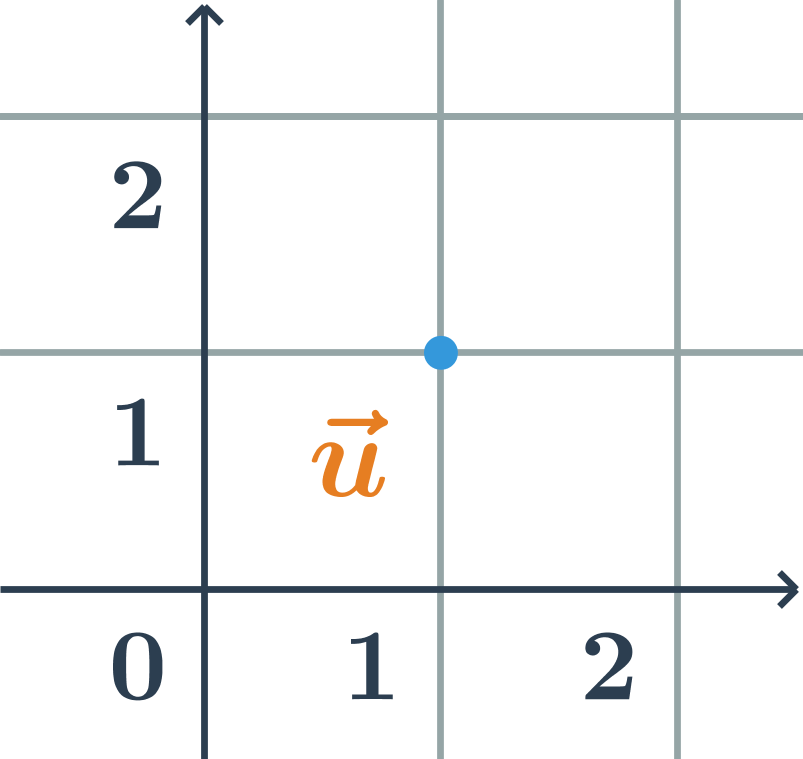
Velikost vektoru $\vec{u}$ = (u₁;u₂) určíme s využitím Pythagorovy věty: | $\vec{u}$ | = √u²₁ + u²₂

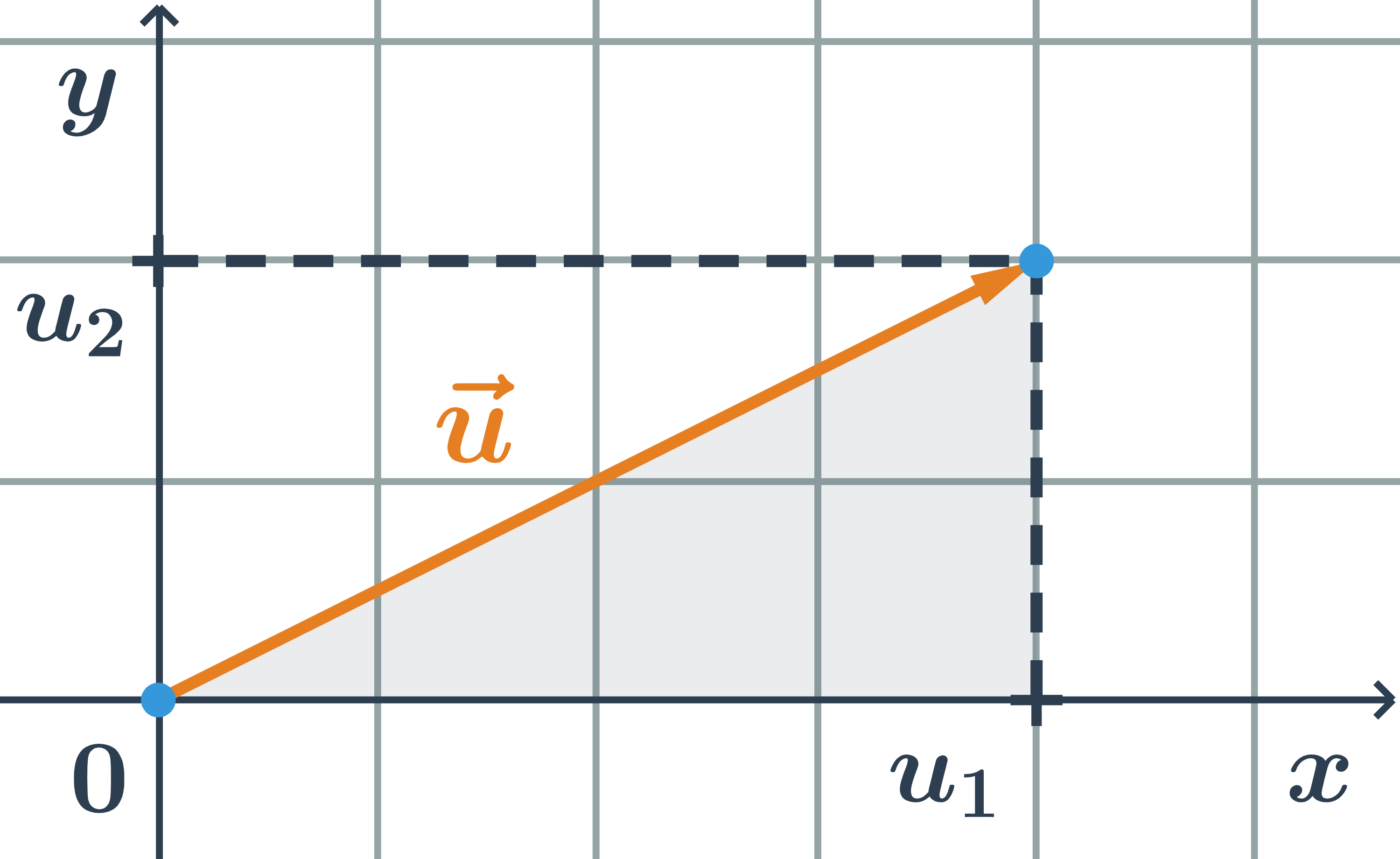
Ve vybarveném trojúhelníku je délka vektoru přepona, odvěsny mají délky u₁ a u₂

Vzájemná poloha vektorů

Opačné vektory jsou vektory, které mají stejnou délku a opačnou orientaci. K vektoru $\vec{u}$ = (u₁;u₂) je opačný vektor $\vec{v}$ = (-u₁;-u₂)

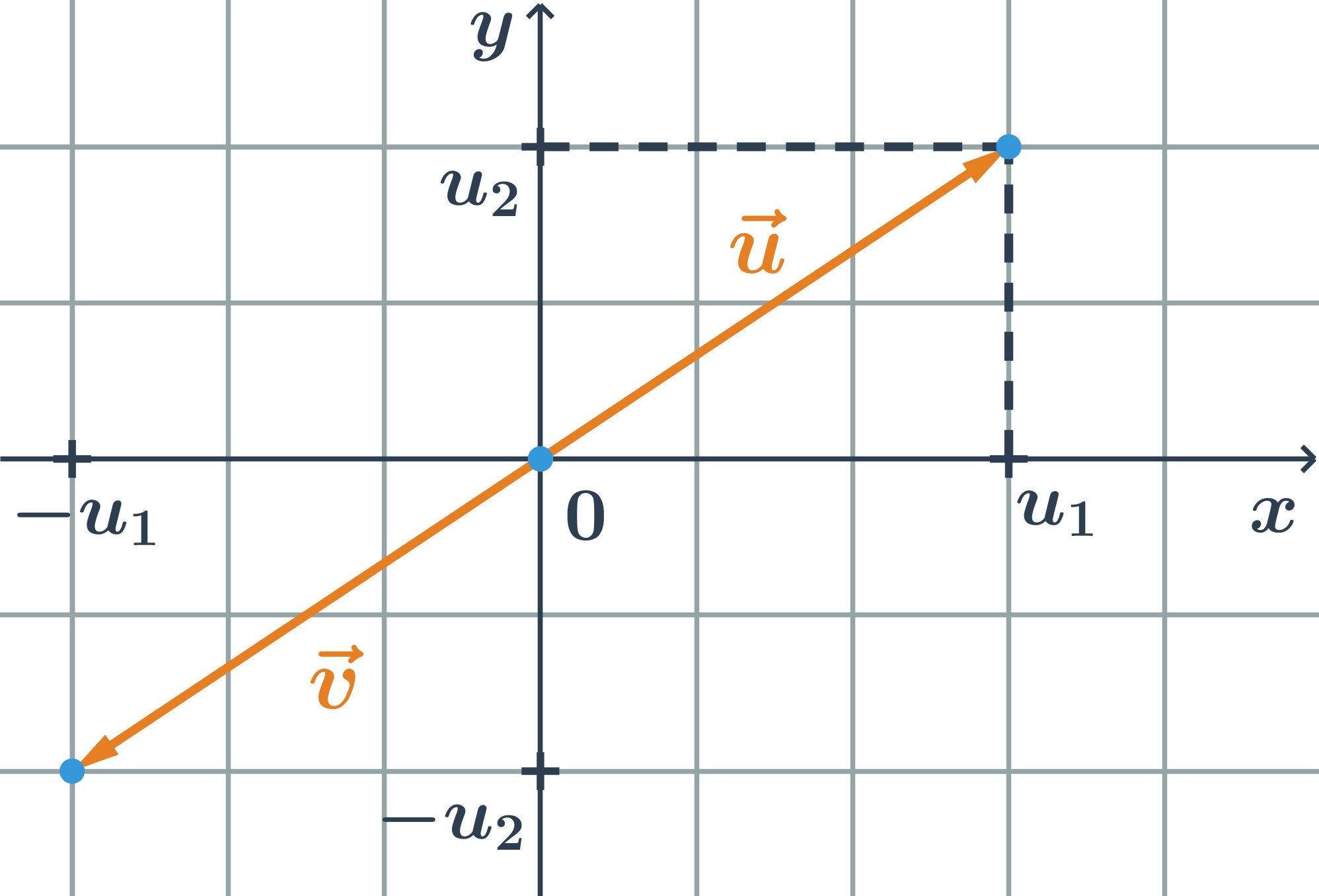
Kolineární vektory jsou vektory, které můžeme umístit na jednu přímku. S vektorem $\vec{u}$ = (u₁;u₂) $\vec{v}$ = (k * u₂;k * u₂), kde k je reálné nenulové číslo. Pro k > 0 vektory mají stejný směr, pro k < 0 mají vektory opačný směr.

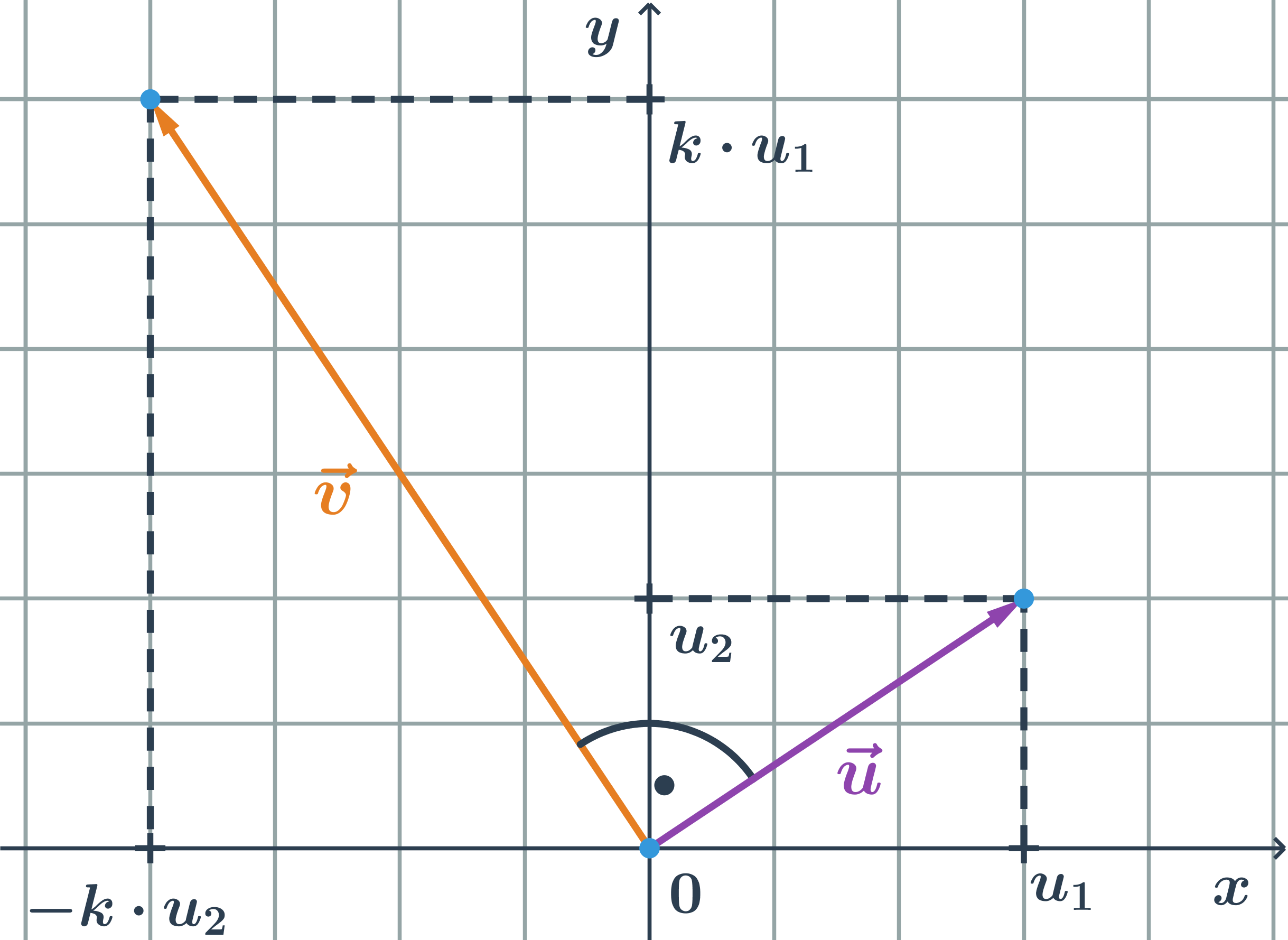
Kolmé vektory jsou vektory, které svírají pravý úhel K vektoru $\vec{u}$ = (u₁;u₂) je kolmý každý vektor $\vec{v}$ = (-k * u₂;k * u₁), kde k je reálné nenulové číslo.

Operace s vektory

Vektory v rovině mohou být zapsané jako dvojice čísel – souřadnic v rovině, podobně trojrozměrné vektory lze zapsat jako trojice čísel – souřadnic v prostoru.

Operace jako součet, rozdíl a vynásobení reálným číslem, které umíme jednoduše provádět s čísly, lze s vektory provádět po jednotlivých souřadnicích. Tím se zabývá kapitolka Vektory: násobení konstantou, součet, rozdíl. Příklady praktického použití těchto operací s vektory:

vrabec letí stejným směrem jako moucha a dvakrát rychleji než moucha – vektor rychlosti vrabce získáme, když vektor rychlosti mouchy vynásobíme konstantou 2,
satelitní snímky ukazují, že ráno ještě vozítko Marka Watneyho stálo na marsovské základně, za dnešek ujel 50 km na východ – jeho novou polohu získáme, když k souřadnicím základny přičteme vektor (50;0),
šnek přelezl rovně po monitoru z levého horního rohu (souřadnice v pixelech [0;0]) do bodu [1007;555] – vektor, jehož souřadnice jsou počty pixelů, co šnek ulezl v horizontálním a vertikálním směru získáme jako rozdíl jeho umístění na konci pohybu a jeho umístění na začátku pohybu.

Speciální operace, kterou lze provést se dvěma vektory stejné dimenze (mají stejný počet souřadnic), je skalární součin. Vstup této operace jsou dva vektory, výstup je reálné číslo.

Díky skalárnímu součinu můžeme vypočítat kupříkladu jaký úhel vektory svírají, speciálně jestli jsou na sebe kolmé (v takovém případě jejich skalární součin vyjde nulový).

Vektory: násobení konstantou, součet, rozdíl

Vektory $\vec{u}$ a $\vec{v}$ sečteme takto: počáteční bod vektoru $\vec{v}$ posuneme do koncového bodu vektoru $\vec{u}$ Součet vektorů $\vec{u}$ a $\vec{v}$ je vektor $\vec{w}$ který má počáteční bod stejný jako vektor $\vec{u}$ a koncový bod stejný jako vektor $\vec{v}$ píšeme $\vec{u}$ + $\vec{v}$ = $\vec{w}$

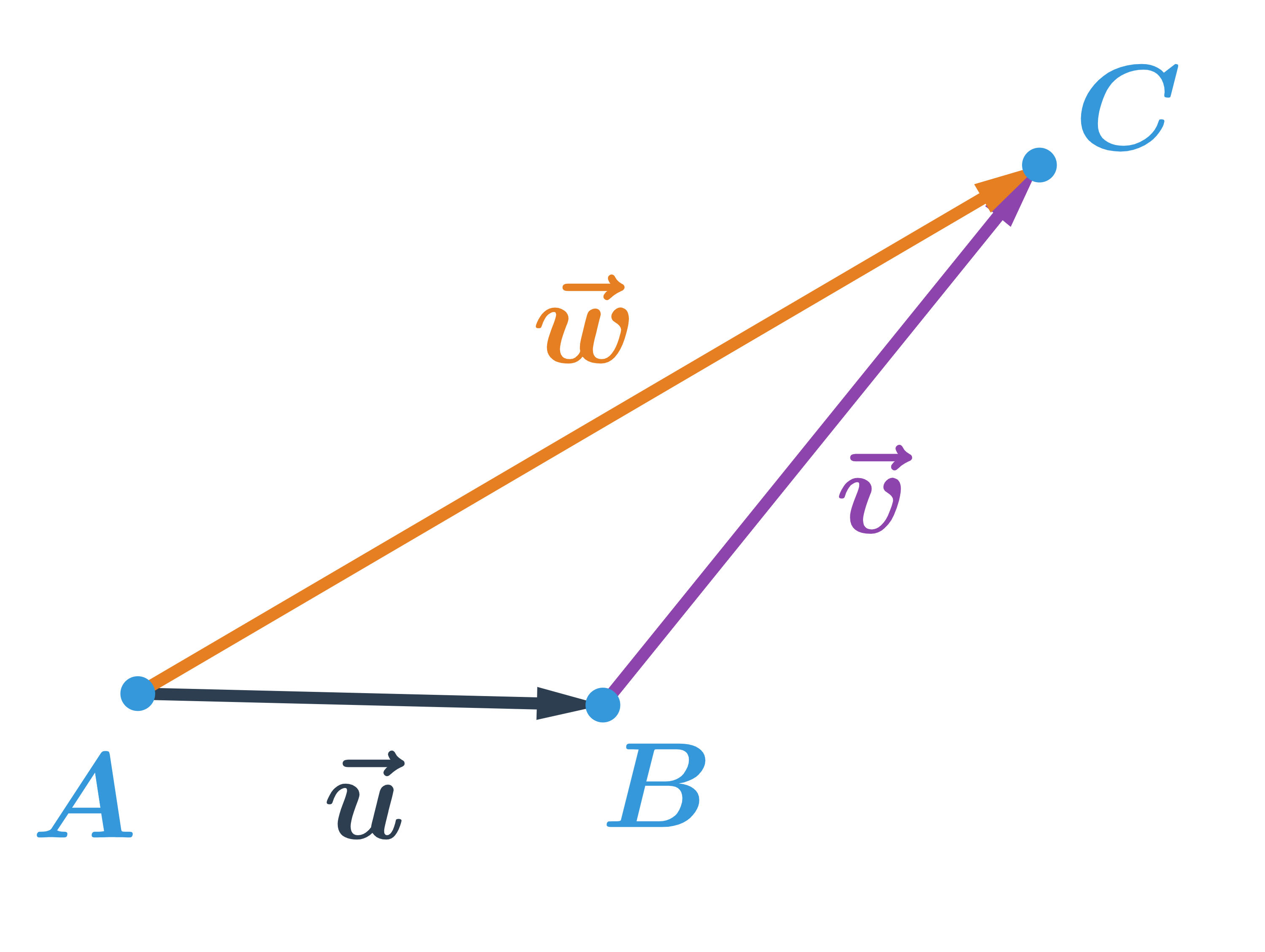
$\vec{u}$ = $\vec{AB}$ , $\vec{v}$ = $\vec{BC}$ .Součet těchto vektorů: $\vec{AB}$ + $\vec{BC}$ = $\vec{AC}$

Mějme vektory se souřadnicemi $\vec{u}$ = (u₁;₂), $\vec{v}$ = (v₁;v₂). Pak součet vektorů $\vec{u}$ a $\vec{v}$ je vektor $\vec{w}$ se souřadnicemi $\vec{w}$ = (u₁ + v₁;u₂ + v₂).

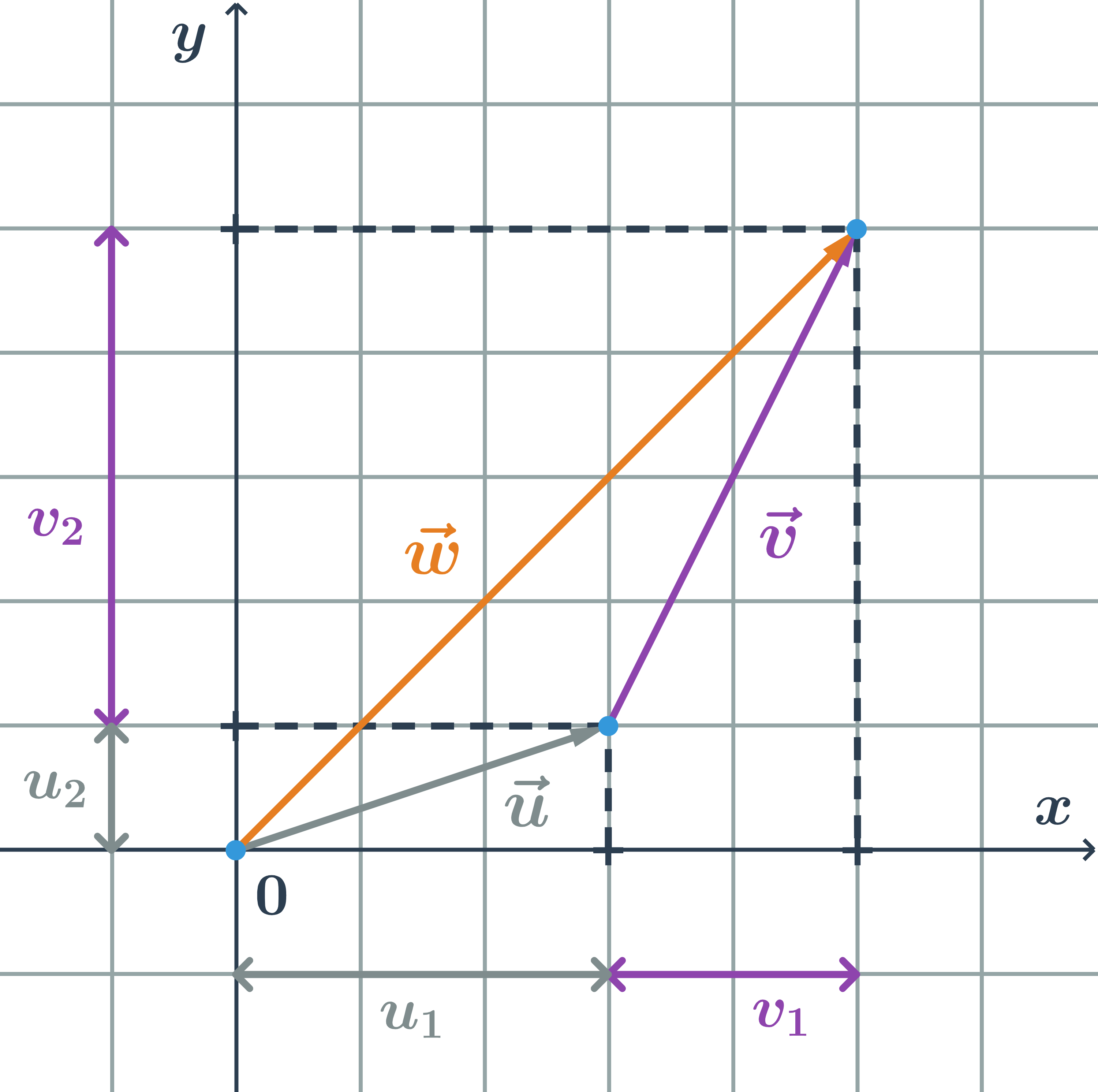
Rozdíl vektorů

Rozdíl vektorů $\vec{u}$ a $\vec{v}$ je součet vektorů $\vec{u}$ s vektorem opačným k $\vec{v}$ . Tedy:

$\vec{u}$ - $\vec{v}$ = $\vec{u}$ + (- $\vec{v}$ )

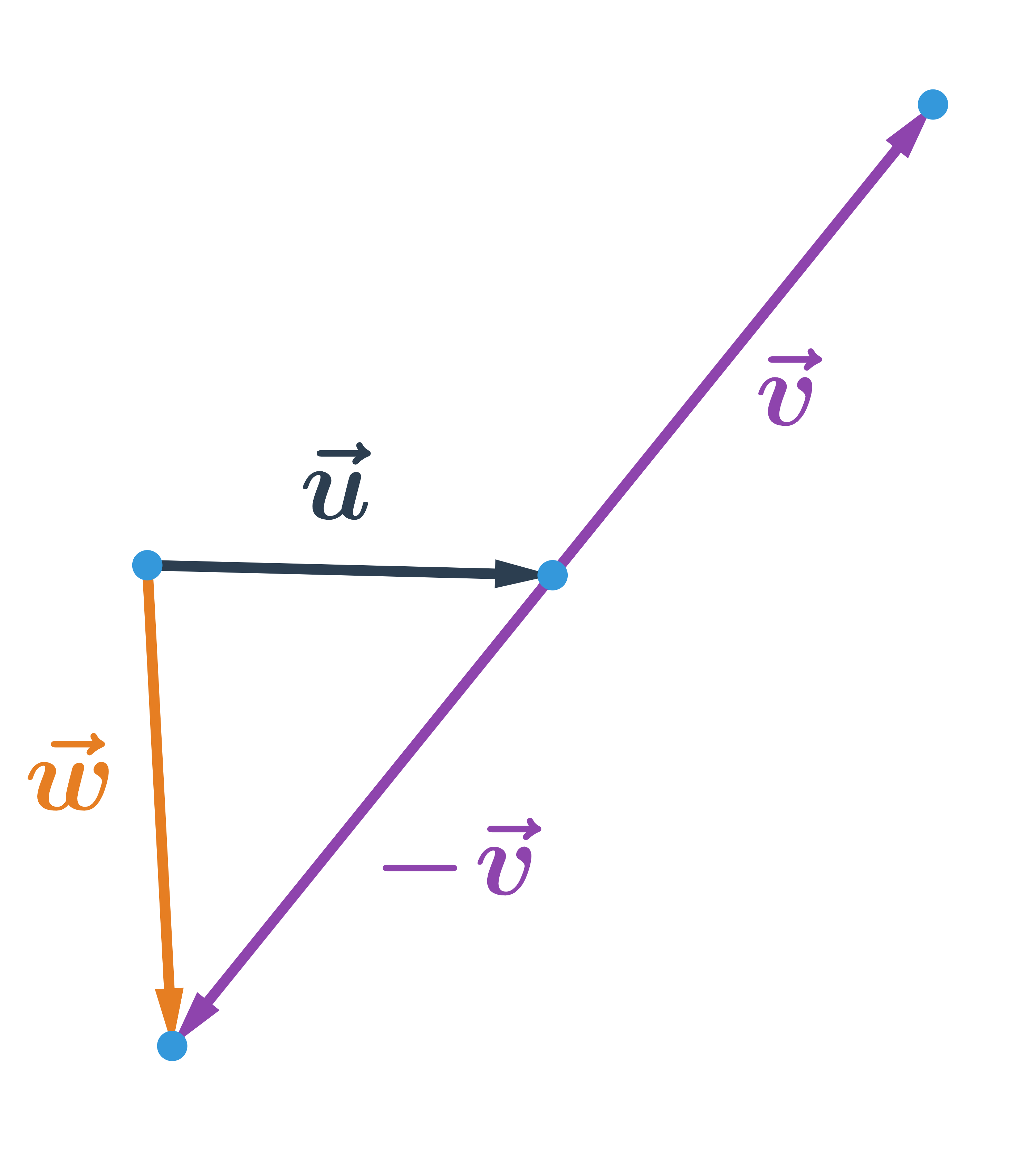
Máme-li souřadnice vektorů: $\vec{u}$ = (u₁;u₂), $\vec{v}$ = (v₁;v₂), pak rozdíl vektorů $\vec{u}$ a $\vec{v}$ je vektor $\vec{w,}$ který má souřadnice: $\vec{w}$ (u₁ - v₁;u₂ - v₂)

Násobek vektoru

Vektor $\vec{u}$ můžeme vynásobit libovolným reálným číslem $k.$ Dostaneme vektor $\vec{v,}$ kterému říkáme násobek vektoru. Píšeme $\vec{v}$ = $\vec{k}$ * $\vec{u}$

Pokud k > 0, vektory $\vec{u}$ a k * $\vec{u}$ mají stejný směr
pokud k < 0, vektory $\vec{u}$ a k * $\vec{u}$ mají opačný směr
Pokud k = 0, vektor k * $\vec{u}$ je nulový vektor

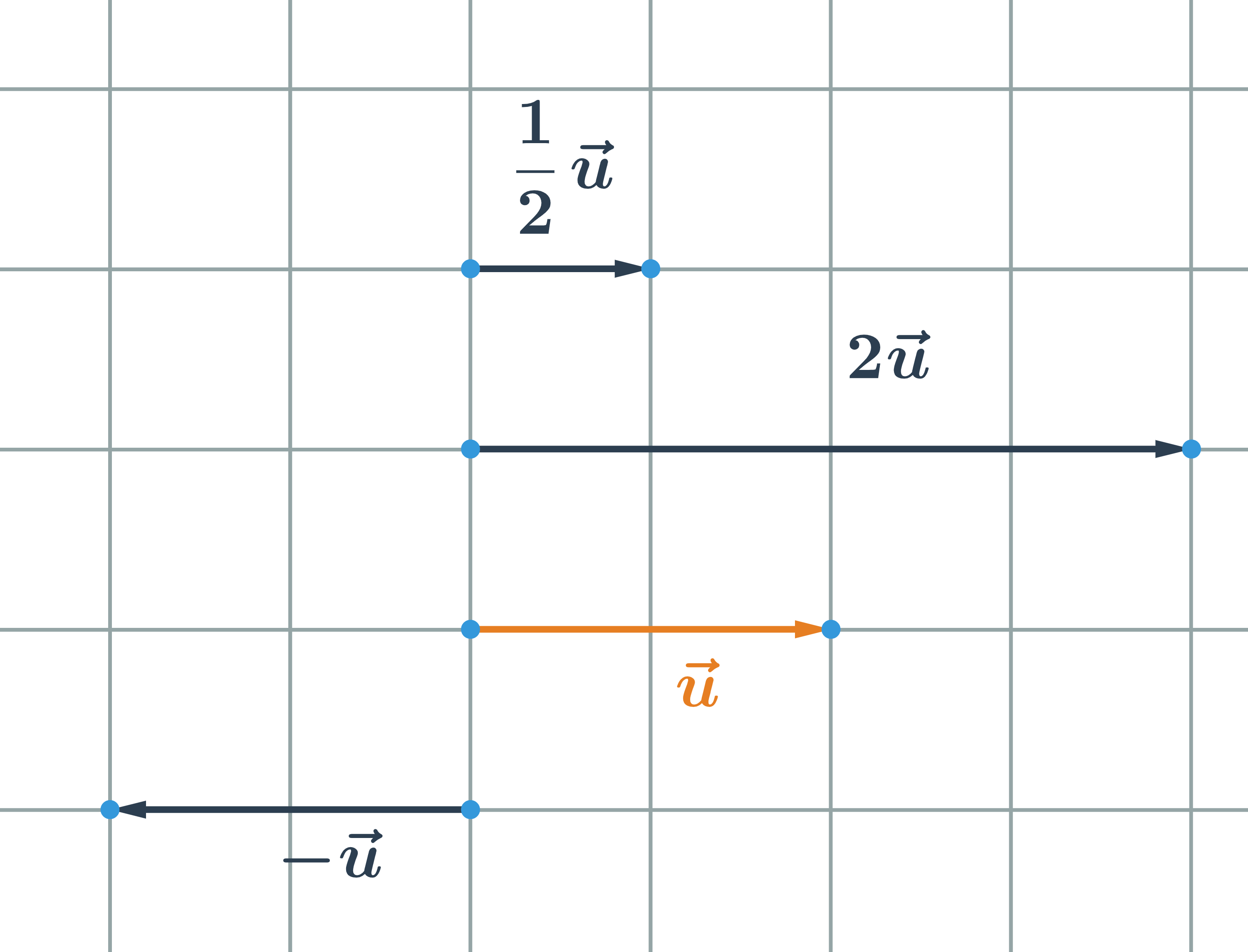
Máme-li souřadnice vektoru $\vec{u}$ = (u₁;u₂), pak jeho násobek $\vec{v}$ = k * $\vec{u}$ má souřadnice $\vec{v}$ = (k * u₁;k * u₂).

Vektory: skalární součin

Skalární součin vektorů $\vec{u}$ a $\vec{v}$ označujeme $\vec{u}$ * $\vec{v.}$ Pro vektory $\vec{u,}$ $\vec{v}$ o velikostech | $\vec{u}$ | a | $\vec{v}$ | které spolu svírají úhel α, je skalární součin definován následovně:

$\vec{u}$ * $\vec{v}$ = | $\vec{u}$ | * | $\vec{v}$ | * cos α

Vlastnosti skalárního součinu

Výsledkem skalárního součinu dvou vektorů je číslo (neboli skalár).
Skalární součin nulového vektoru s libovolným jiným vektorem je vždy roven 0
Skalární součin vektorů, které jsou na sebe kolmé, je také roven nule.

Výpočet pomocí souřadnic

Máme-li souřadnice vektorů $\vec{u}$ = (u₁;u₂), $¨ \vec{v}$ = (v₁;v₂), pak hodnota jejich skalárního součinu je:

u₁ * v₁ + u₂ * v₂

Určení úhlu svíraného dvěma vektory

S využitím vztahu pro skalární součin můžeme určit úhel vektorů: cos α = $\frac{\vec{u} \cdot \vec{v}}{| \vec{u} | \cdot | \vec{v} |}$

Přímky

Přímka je jednoznačně určena bodem, který na ní leží a směrovým vektorem, což si můžete prakticky vyzkoušet v kapitole Určení přímky.

V rovině i v prostoru lze zapsat přímku jako množinu bodů, které splňují parametrickou rovnici. V rovině umíme pro danou přímku napsat také obecnou rovnici (ale v prostoru ne).

Máme-li přímku popsanou rovnicí, umíme určit vzájemnou polohu dvou přímek nebo vzájemnou polohu přímky a bodu výpočtem.

Přímky: pojmy

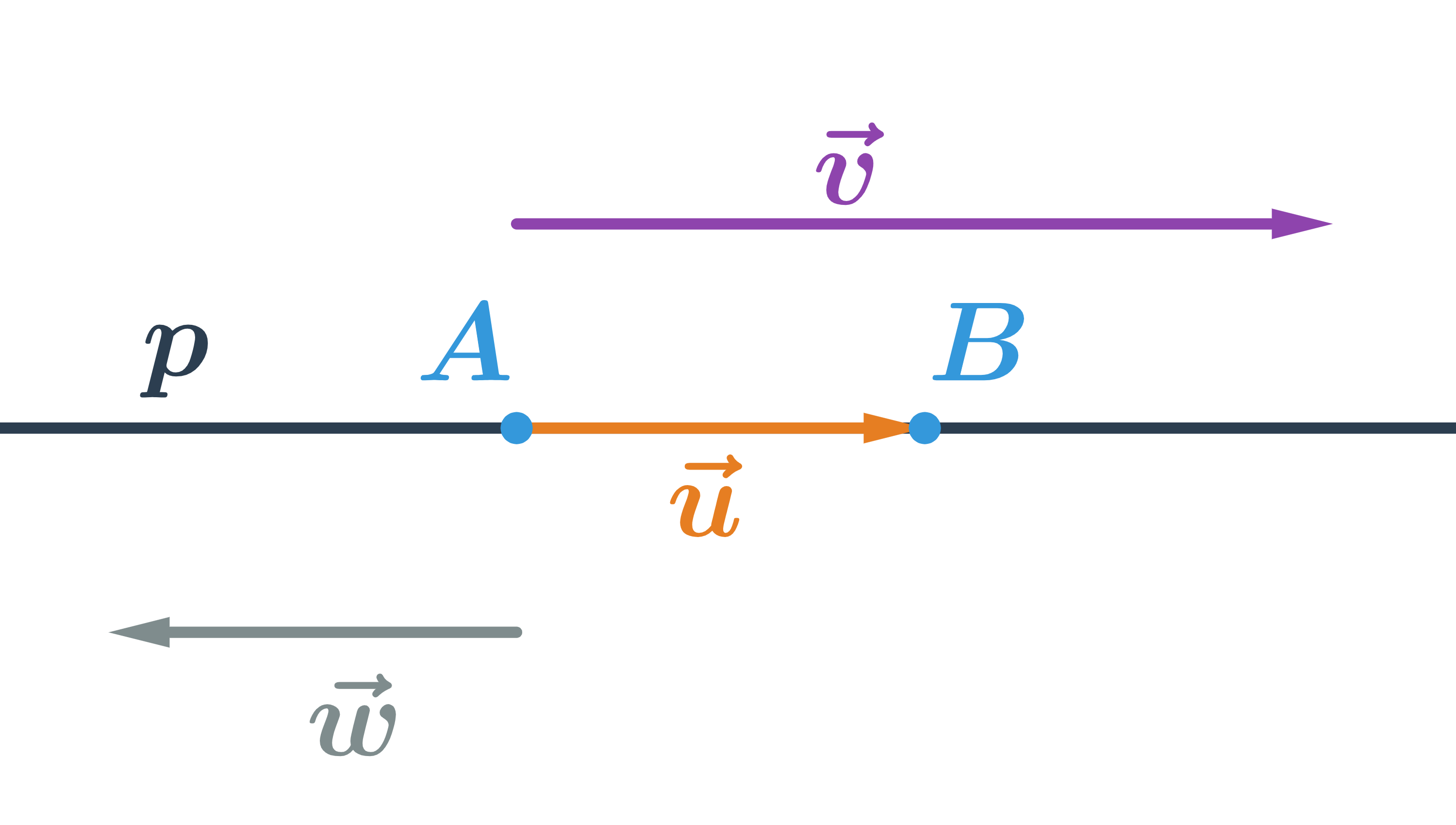
Přímka je jednoznačně určena dvěma body, na obrázku je přímka p určená body A a B. Každý vektor, který je rovnoběžný s vektorem $\vec{AB}$ se nazývá směrový vektor přimky p. Kterýkoliv z vektorů na obrázku je směrový vektor přímky p. K tomu, abychom určili konkrétní přímku ještě potřebujeme znát jeden bod na přímce (přímka p na obrázku je určena bodem A a kterýmkoliv z vektorů $\vec{u,}$ $\vec{v,}$ $\vec{w}$ ).

Parametrické rovnice přímky

Přímka určená bodem A = (a₁;a₂) a vektorem $\vec{u}$ = (u₁;u₂) má parametrické rovnice tvaru: x = a₁ + t ⋅ u₁
y = a₂ + t ⋅ u₂
t e R

Zkráceně můžeme vyjádřit p : A + t $\vec{u,}$ číslo t nazýváme parametr.

Obecná rovnice přímky

Každý vektor kolmý k přímce p se nazývá normálový vektor přímky p. Obecná rovnice přímky je rovnice ve tvaru: ax + by + c = 0, kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo.

Bod a přímka

Bod M = [m₁;m₂] leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky. Pokud je přímka daná obecnou rovnicí ax + by + c = 0, pro souřadnice bodu, který leží na přímce platí: a ⋅ m₁ + b ⋅ m₂ + c = 0 Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t.

Dvě přímky

Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné.

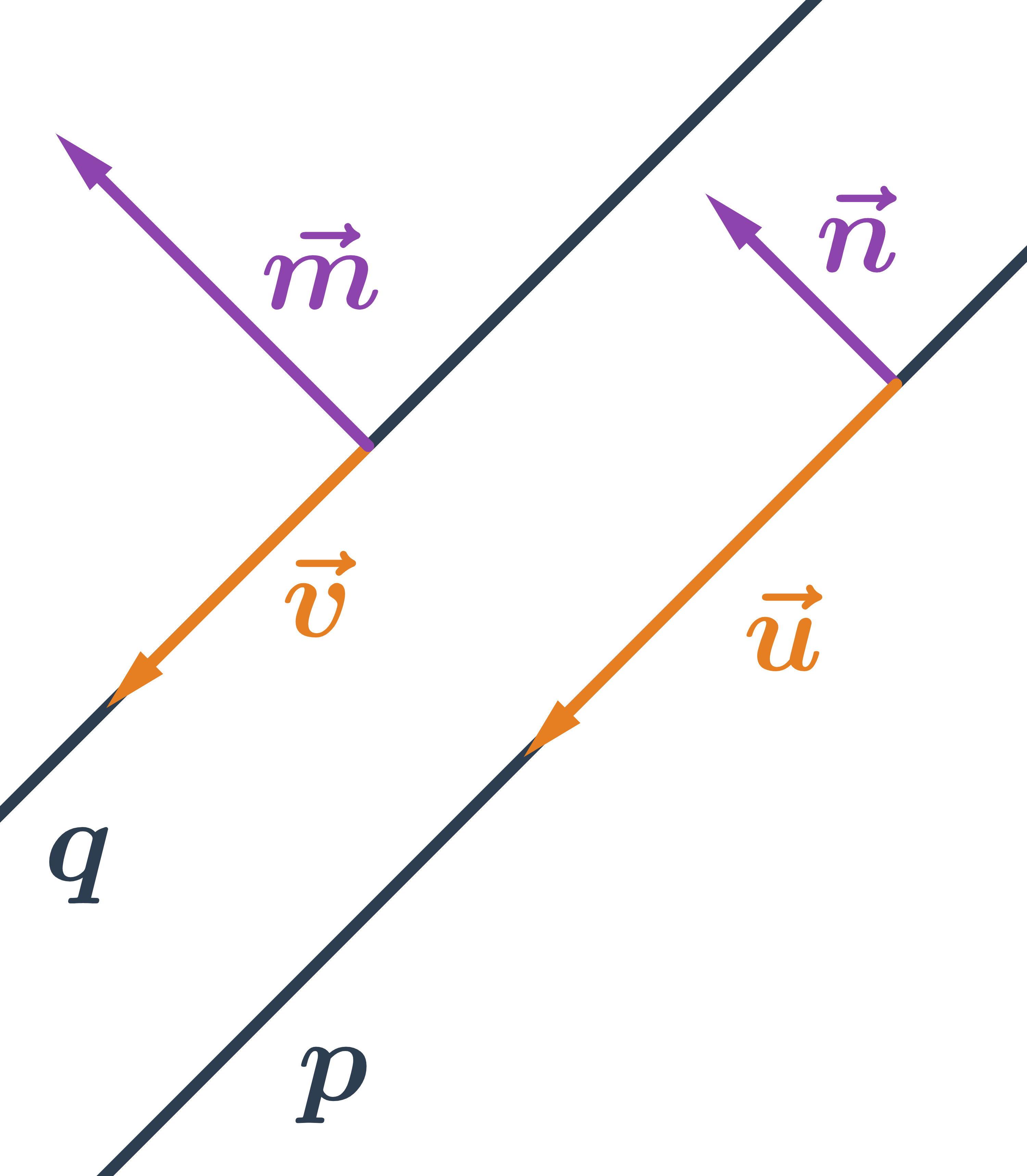
Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.

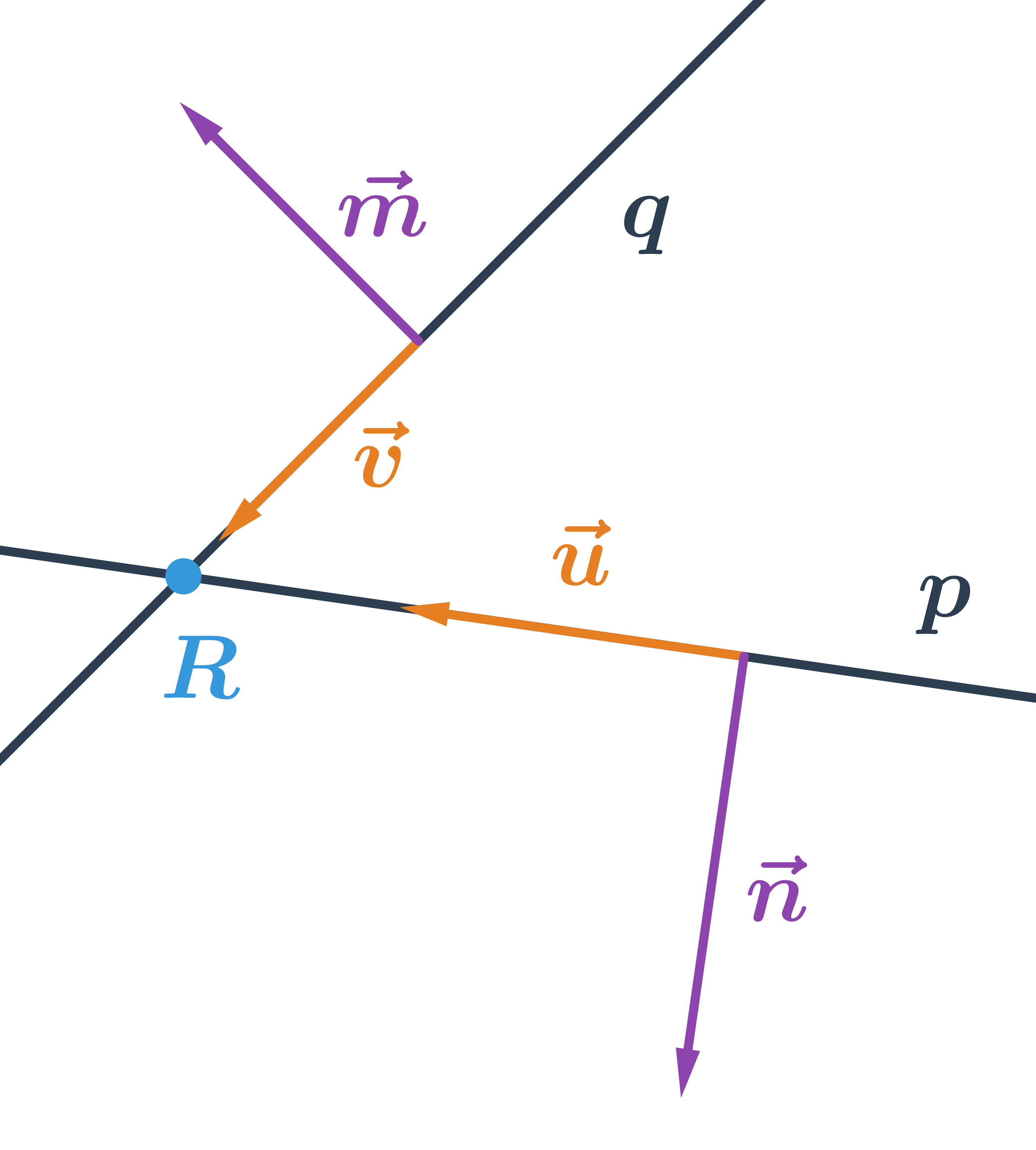
Přímka v prostoru

Přímku v prostoru nelze vyjádřit obecnou rovnicí. Parametrickou rovnici přímky v prostoru určíme obdobně jako v rovině na základě znalosti souřadnic směrového vektoru a jednoho bodu na přímce.

Určení přímky

Přímka je obvykle určena bodem a vektorem, případně dvěma body.

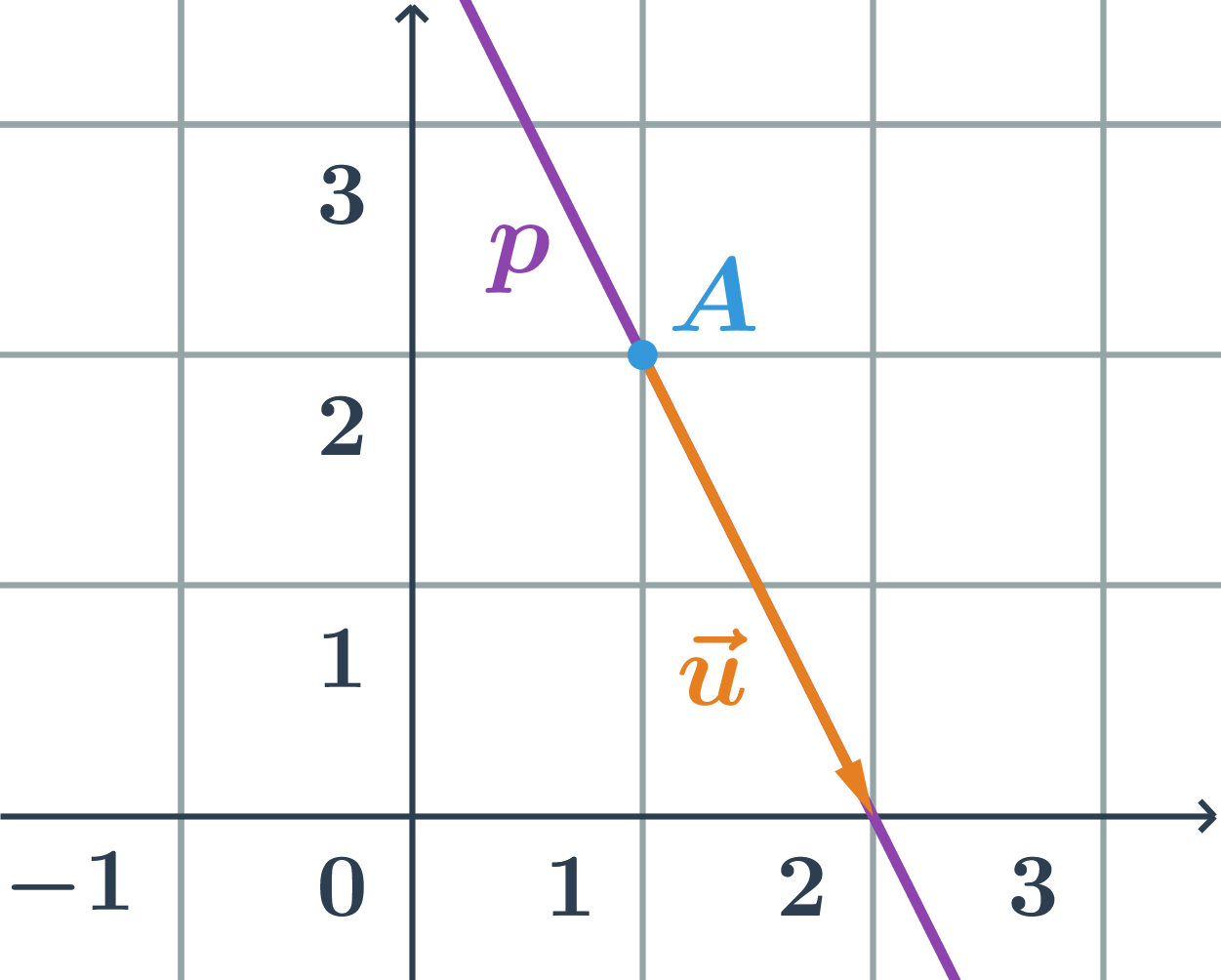
přimka p na obrázku je určena například:

bodem A = [1;2], který na ní leží a směrovým vektorem $\vec{u}$ = (1;-2)
nebo dvěma různými body [1;2] a [2;0], které na ní leží

Parametrické rovnice přímky v rovině

Přímka určená bodem A = [a₁;a₂] a směrovým vektorem $\vec{u}$ = (u₁;u₂) má parametrické rovnice tvaru:

x = a₁ + t ⋅ u₁
y = a₂ + t ⋅ u₂
t ∈ R

Zkráceně můžeme vyjádřit p : X = A + t $\vec{u,}$ číslo t nazýváme parametr. Pokud známe dva body A, B ležící na přímce, směrový vektor je například $\vec{u}$ = $\vec{AB.}$

Obecná rovnice přímky v rovině

Obecná rovnice přímky v rovině má tvar: ax + by + c = 0 kde konstanty a a b jsou souřadnice normálového vektoru a c reálné číslo. Normálový vektor $\vec{u}$ = (a;b) je vektor kolmý k dané přímce, tedy i kolmý ke směrovému vektoru přímky

Směrnicový tvar rovnice přímky

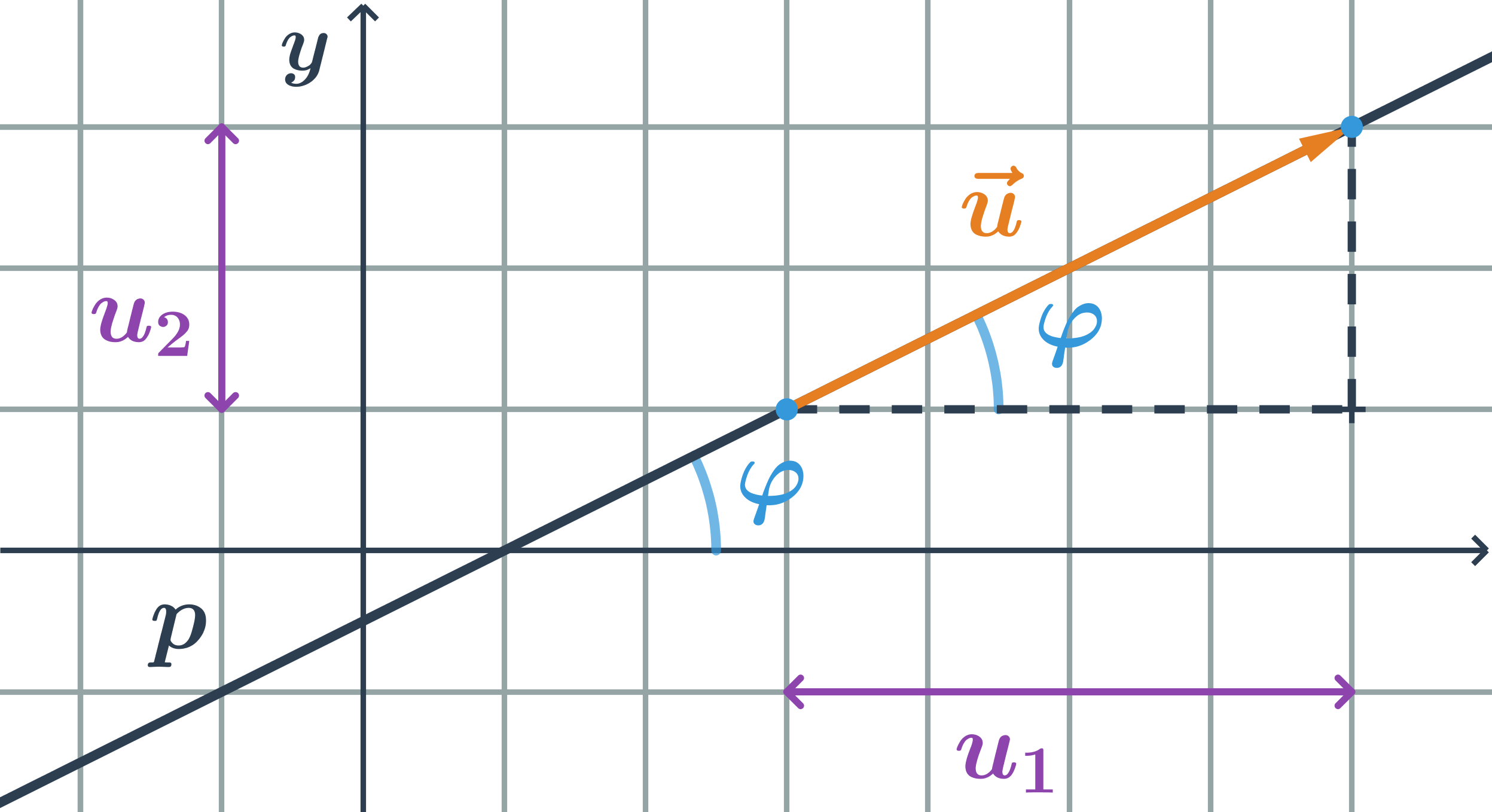
Každou přímku p, která není rovnoběžná s osou y můžeme vyjádřit ve tvaru: y = kx + q, kde k, q ∈ R

Tento tvar se nazývá směrnicový tvar rovnice přímky.

Konstanta k se nazývá směrnicea její hodnota je tangens úhlu, který svírá přímka p s kladnou částí osy x, tedy: k = tan φ.

Konstanta q určuje průsečík přímky p s osou y, souřadnice průsečíku jsou: P = [0;q]. Pro přímku, která prochází počátkem je q = 0, tedy směrnicový tvar její rovnice je: y = kx

Směrnice přímky, která má směrový vektor $\vec{u}$ = (u₁;u₂) je podíl souřadnic směrového vektoru:
k = tan φ = $\frac{u_{1}}{u_{2}}$

Dvě přímky

Dvě rovnoběžné přímky svírají s kladnou částí osy x stejný úhel, mají tedy stejnou směrnici.

Pro dvě k sobě kolmé přímky platí:

přímka p má směrový vektor $\vec{u}$ = (u₁;u₂) a tedy směrnicí: k = $\frac{u_{1}}{u_{2}}$
každá přímka k ní kolmá má směrový vektor (- u₂;u₁) a tedy směrnici: $\frac{u_{1}}{{- u}_{2}}$ = - $\frac{1}{k}$

Vzájemná poloha přímek v rovině

Vzájemnou polohu dvou přímek můžeme snadno určit, pokud známe souřadnice jejich směrových, případně normálových vektorů. Přímky rovnoběžné mají stejný směr, tedy jejich směrové vektory jsou kolineární. Normálové vektory dvou rovnoběžných přímek jsou také kolineární. Ve speciálním případě mohou být přímky totožné. Přímky různoběžné mají jeden společný bod, tento bod musí splňovat rovnice obou přímek. Jejich směrové vektory nejsou kolineární, normálové vektory také nejsou kolineární.

Souvislost počtu společných bodů přímek s počtem řešení soustavy rovnic

Pro určení společného bodu (bodů) dvou přímek, vždy řešíme soustavu rovnic. Tato soustava může mít:

jedno řešení – přímky jsou různoběžné
žádné řešení – přímky jsou rovnoběžné
nekonečně mnoho řešení - přímky jsou totožné

Vzájemná poloha přímky a bodu v rovině

Bod leží na přímce, jestliže jeho souřadnice vyhovují rovnici přímky.

Pokud je přímka daná obecnou rovnicí, po dosazení souřadnic bodu, který na přímce leží, do rovnice přímky nastane rovnost
Pokud je přímka daná parametricky, po dosazení souřadnic bodu vychází z obou rovnic stejná hodnota parametru t.

Polohové úlohy

V polohových úlohách řešíme analyticky vzájemnou polohu geometrických útvarů v rovině. Nejčastěji jde o vzájemnou polohu dvou přímek nebo o vzájemnou polohu přímky a bodu.

Metrické úlohy

V metrických úlohách v analytické geometrii bývá úkolem spočítat konkrétní číselnou hodnotu veličin jako je:

vzdálenost dvou objektů, např. vzdálenost bodu od přímky,
odchylka dvou přímek v rovině.

Vzdálenost bodu od přímky

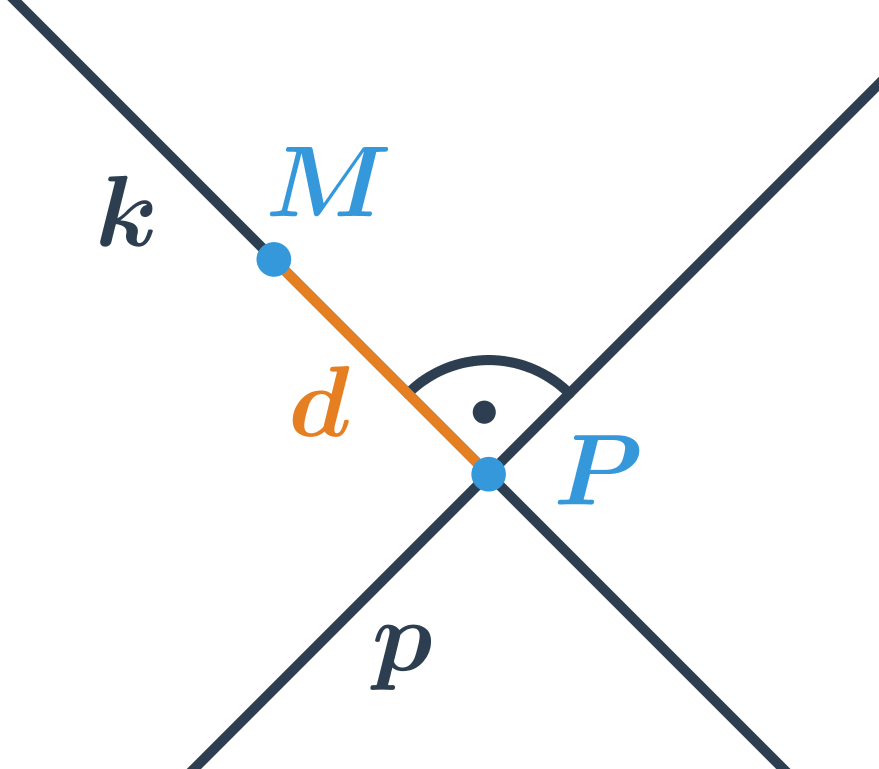
Vzdálenost bodu od přímky je délka nejkratší úsečky určené bodem M a bodem ležícím na přímce p. Jak je vidět z obrázku tato nejkratší úsečka leží na kolmici z bodu M k přímce p. Vzdálenost bodu od přímky tedy můžeme určit takto:

najdeme přímku k, která prochází bodem M a je kolmá k přímce p
určíme průsečík P přímky k s přímkou p
vzdálenost bodu M od přímky p od přímky PM

Vzorec pro vzdálenost bodu od přímky dané obecnou rovnicí

Vzdálenost bodu M = [m₁;m₂] od přímky p dané obecnou rovnicí ax + by + c = 0 je dána vzorcem: d = $\frac{|am₁+bm₂+c|}{√a²+b²}$

Vzdálenost dvou rovnoběžek

Umíme-li určit vzdálenost bodu od přímky, snadno určíme také vzdálenost dvou rovnoběžek. Stačí si uvědomit, že všechny body ležící na jedné přímce mají od druhé přímky stejnou vzdálenost. Proto je vzdálenost rovnoběžek stejná jako vzdálenost libovolného bodu na jedné přímce od přímky druhé.

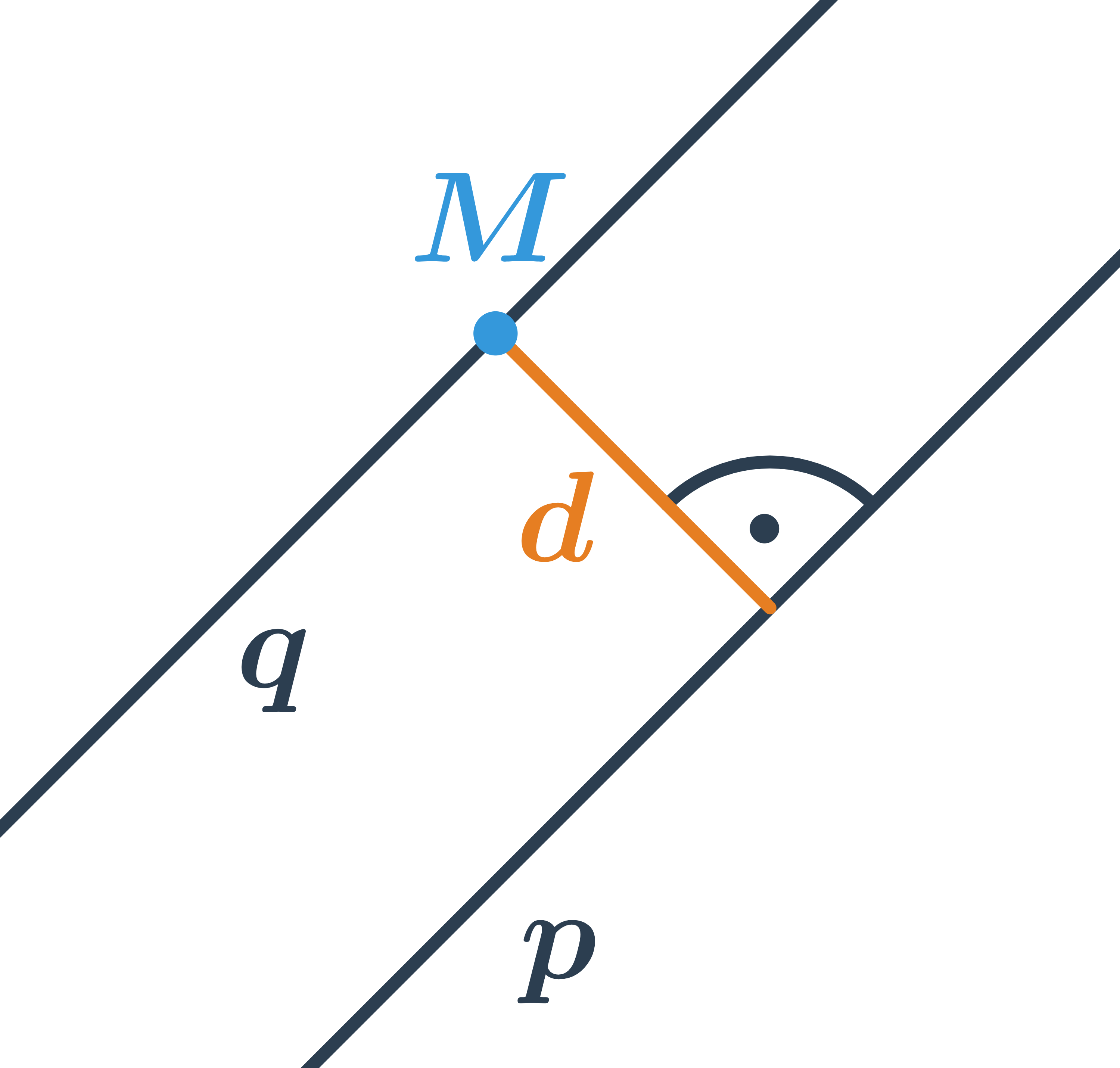
Odchylka dvou přímek

Odchylka rovnoběžek je 0°. Odchylka různoběžek je velikost ostrého nebo pravého úhlu, který přímky svírají.

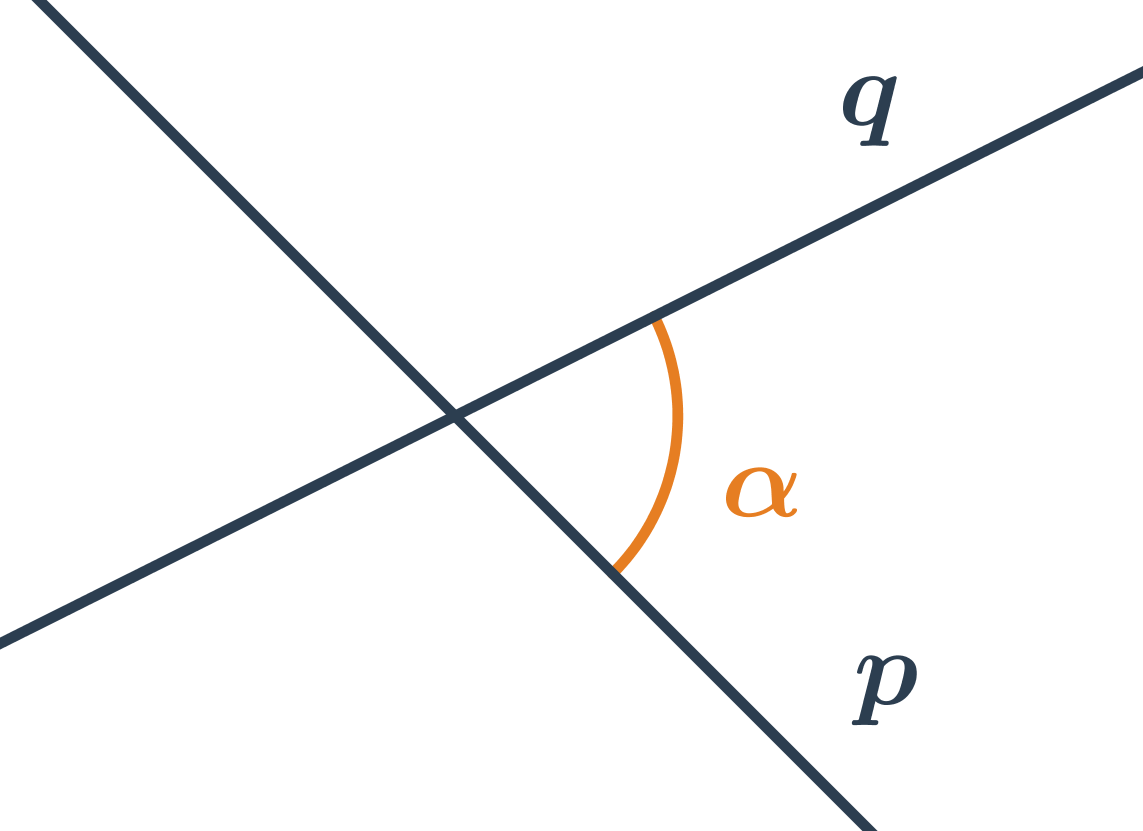
Odchylku různoběžek p a q můžeme vypočítat na základě znalosti směrových nebo normálových vektorů přímek. Vzorec pro výpočet úhlu různoběžek je obdobný jako vzorec pro výpočet úhlu vektorů

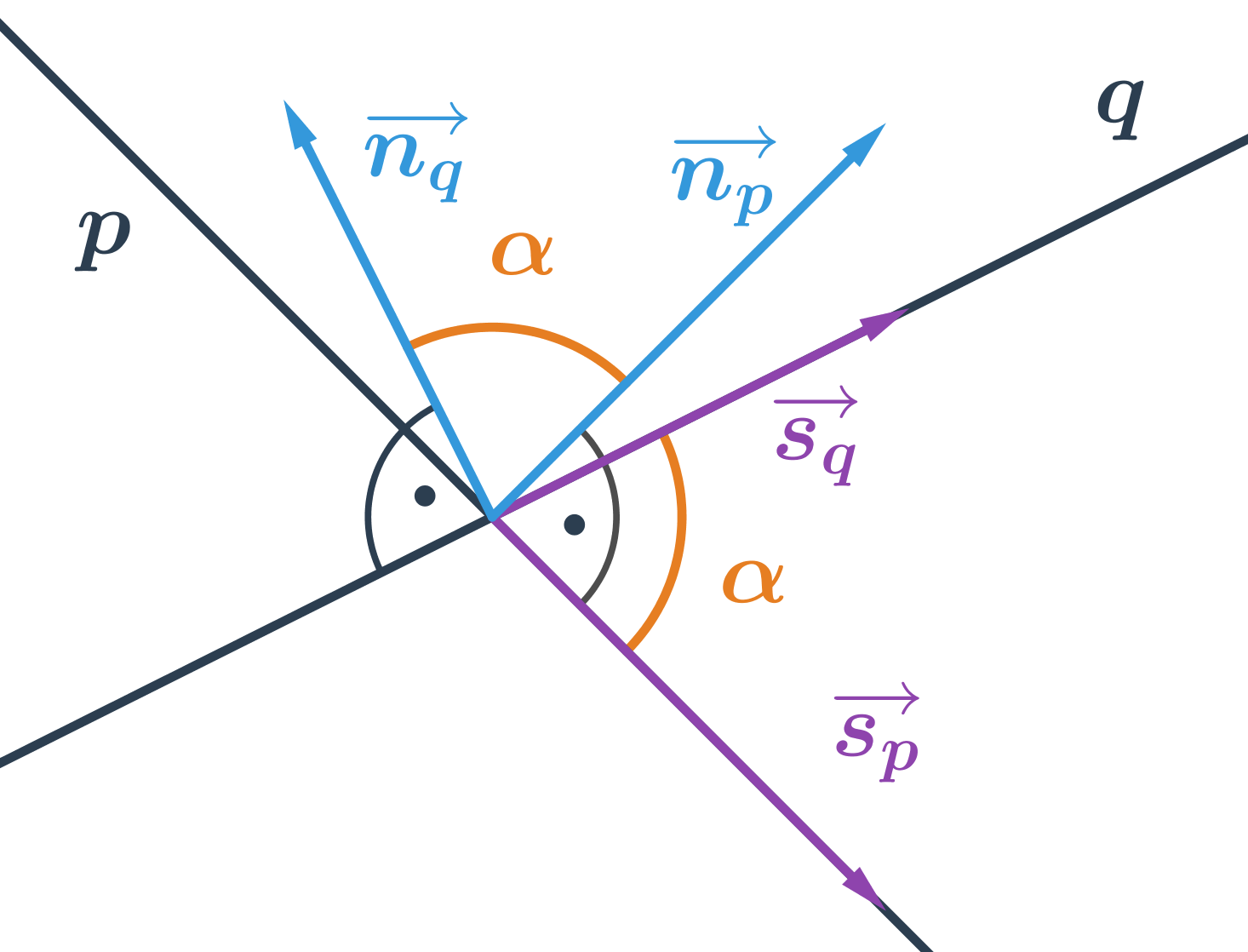
Odchylka různoběžek je úhel α, pro který platí: $\frac{\vec{u} \cdot \vec{v}}{| u | \cdot | v |}$ Vektory $\vec{u}$ a $\vec{v}$ uvedené ve vzorci jsou směrové vektory $\vec{sp⁢}$ a $\vec{sq⁢}$ nebo normálové vektory $\vec{np⁢}$ a $\vec{nq⁢}$ přímek p a q

Pro dvě k sobě kolmé přímky platí, že jejich odchylka α = 90° a tedy cos α = 0.

Roviny

Rovina je určena třemi body, které neleží na jedné přímce. Z předchozích kapitol již víme, že dvojice bodů určuje přímku, případně vektor, proto je mnoho dalších způsobů jak určit rovinu:

bodem a přímkou
dvěma různoběžnými přímkami
dvěma rovnoběžnými přímkami
bodem a dvěma vektory

V prostoru lze zapsat rovinu jako množinu bodů, které splňují parametrickou rovnici nebo obecnou rovnici.

Máme-li rovinu popsanou rovnicí, umíme určit vzájemnou polohu roviny a bodu výpočtem.

Roviny: pojmy

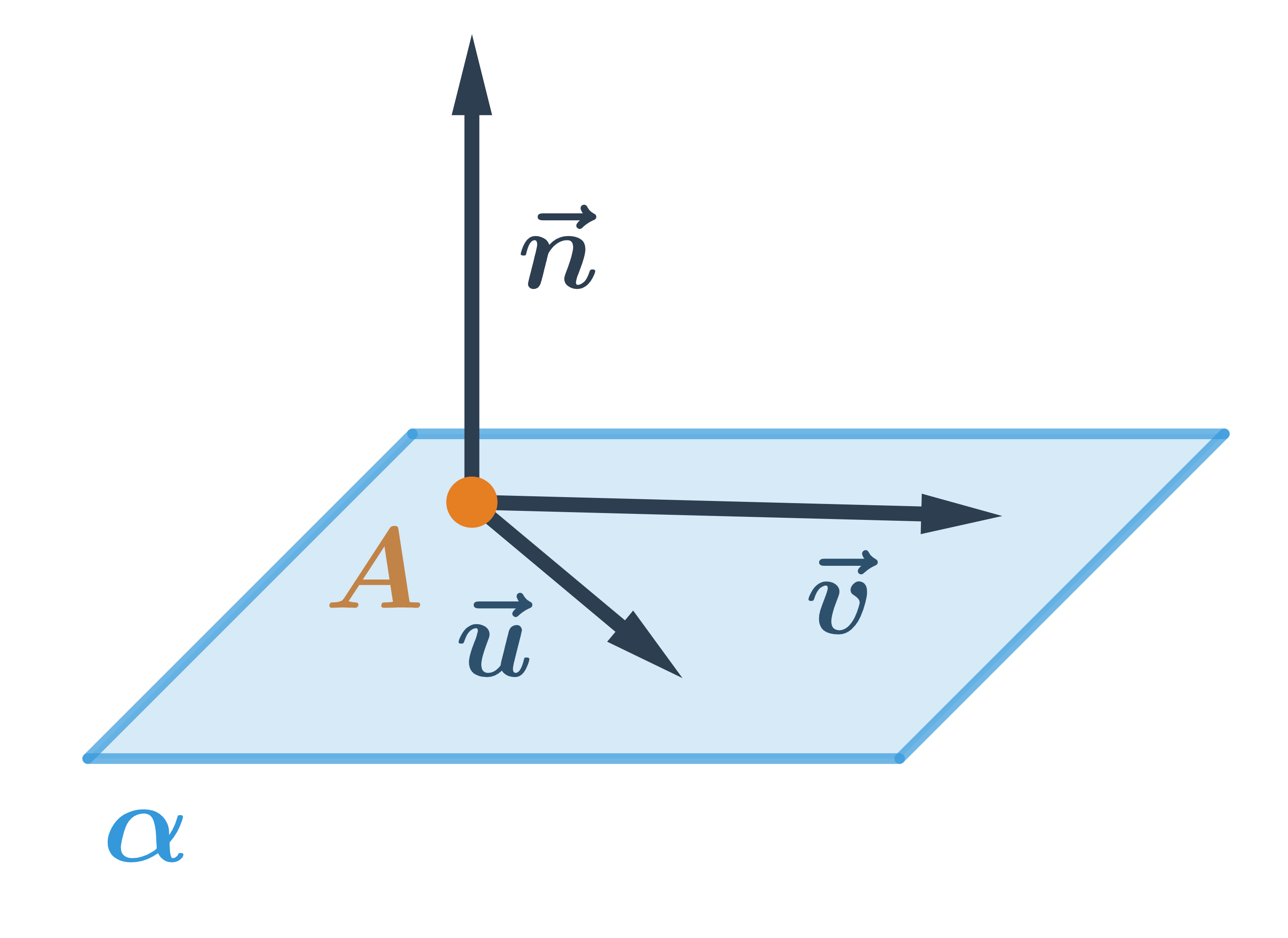
Přímka je jednoznačně určena bodem a dvěma vektory, které nejsou kolineární. Na obrázku je rovina α určená bodem A a vektory $\vec{u}$ , $\vec{v}$ . Každý vektor, který je kolmý k rovině α se nazývá normálový vektor roviny α.Na obrázku je normálový vektor $\vec{n}$ .

Parametrické rovnice roviny

Rovina určená bodem A = [a₁;a₂;a₃] a vektory $\vec{u}$ = [u₁;u₂;u₃] a $\vec{v}$ = [v₁;v₂;₃] má parametrické rovnice ve tvaru:

x = a₁ + t ⋅ u₁ + s ⋅ v₁
y = a₂ + t ⋅ u₂ + s ⋅ v₂
z = a₃ + t ⋅ u₃ + s ⋅ v₃
t, s ∈ R

Zkráceně můžeme vyjádřit α : X = A + $\vec{tu}$ + $\vec{sv}$ kde t, s ∈ R jsou parametry.

Obecná rovnice roviny

Obecná rovnice roviny má tvar ax + by + cz + d = 0, kde konstanty a, b, c jsou souřadnice normálového vektoru a d reálné číslo. Normálový vektor $\vec{n}$ = (a;b;c) je vektor kolmý k dané rovině.

Vzájemná poloha bodu a roviny

Bod leží v rovině, jestliže jeho souřadnice vyhovují rovnici roviny. Pokud je rovina daná obecnou rovnicí, po dosazení souřadnic bodu do rovnice roviny nastane rovnost. Pokud je rovina daná parametricky, po dosazení souřadnic bodu dostaneme soustavu tří rovnic pro dvě neznámé, která má právě jedno řešení.

Kuželosečky

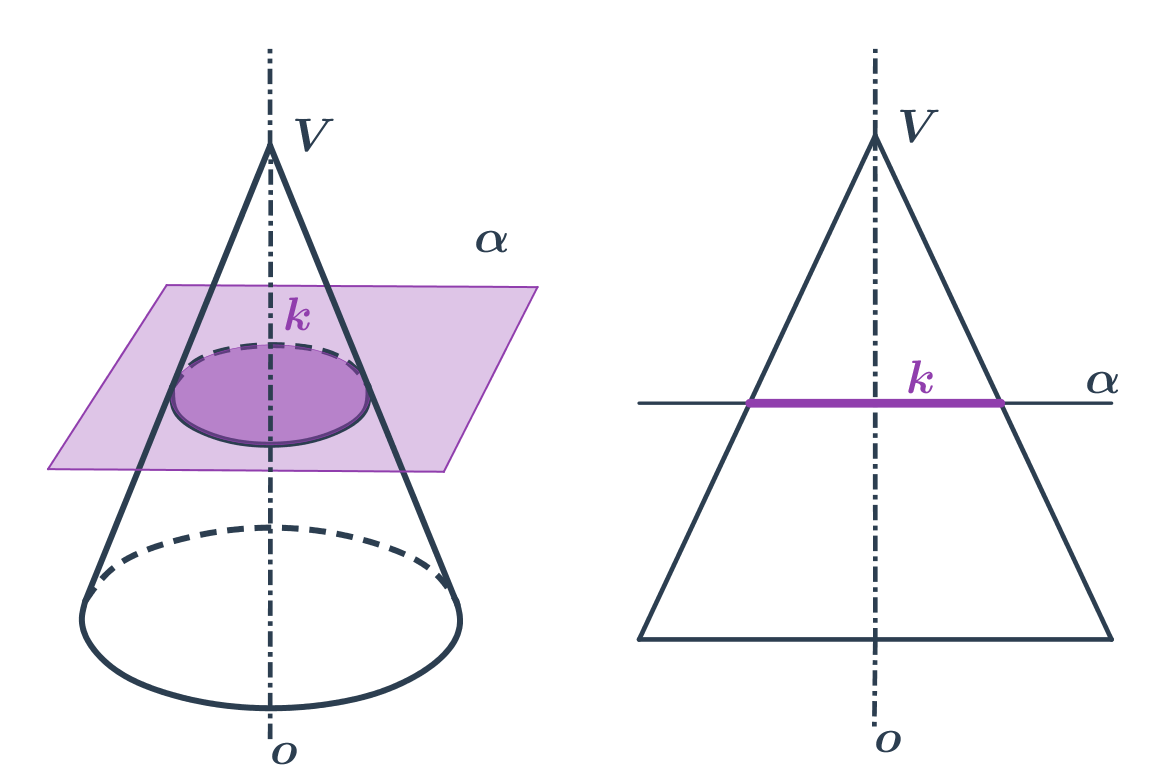
Jak již název napovídá, mají kuželosečky společný původ. Vzniknou jako řez rotační kuželové plochy rovinou.

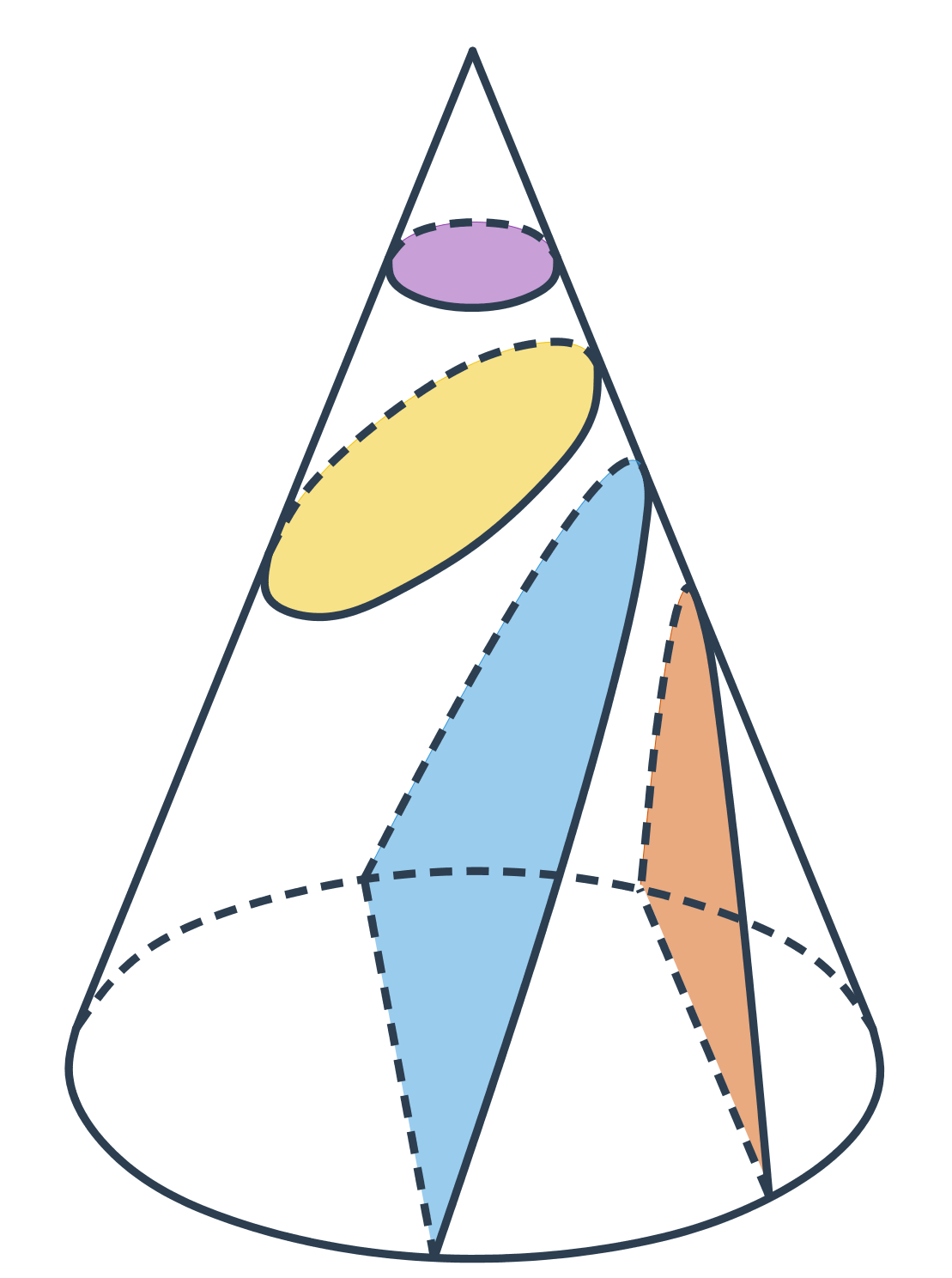
Kružnice vznikne řezem roviny kolmé na osu kuželové plochy.
Pokud rovinu řezu trochu nakloníme, vznikne elipsa.

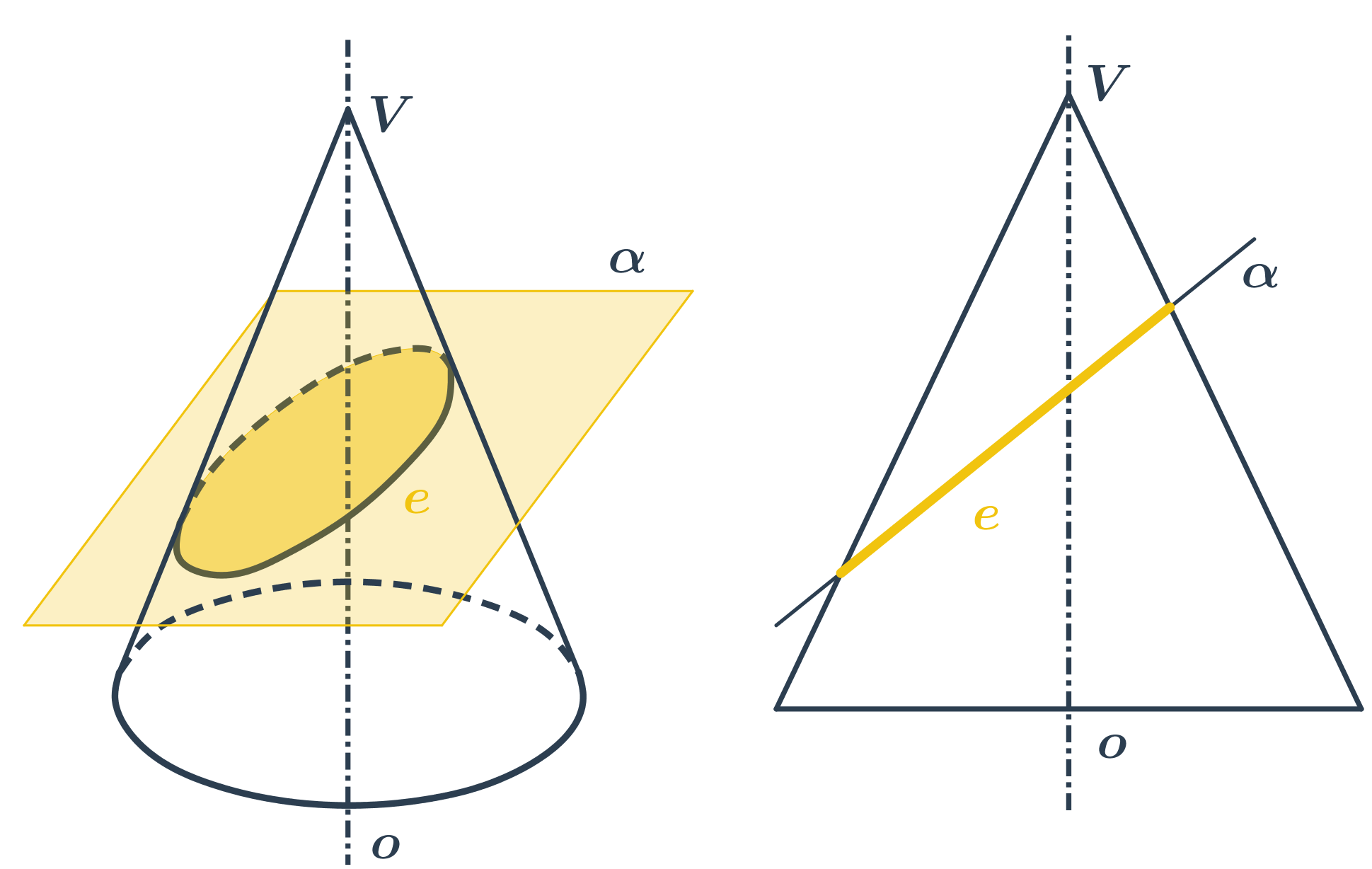
Pokud rovinu řezu nakloníme tolik, že bude rovnoběžná s některou z přímek na kuželové ploše, vznikne parabola.
Při dalším naklánění už rovina řezu protne obě části kuželové plochy a vznikne dvoudílná hyperbola.

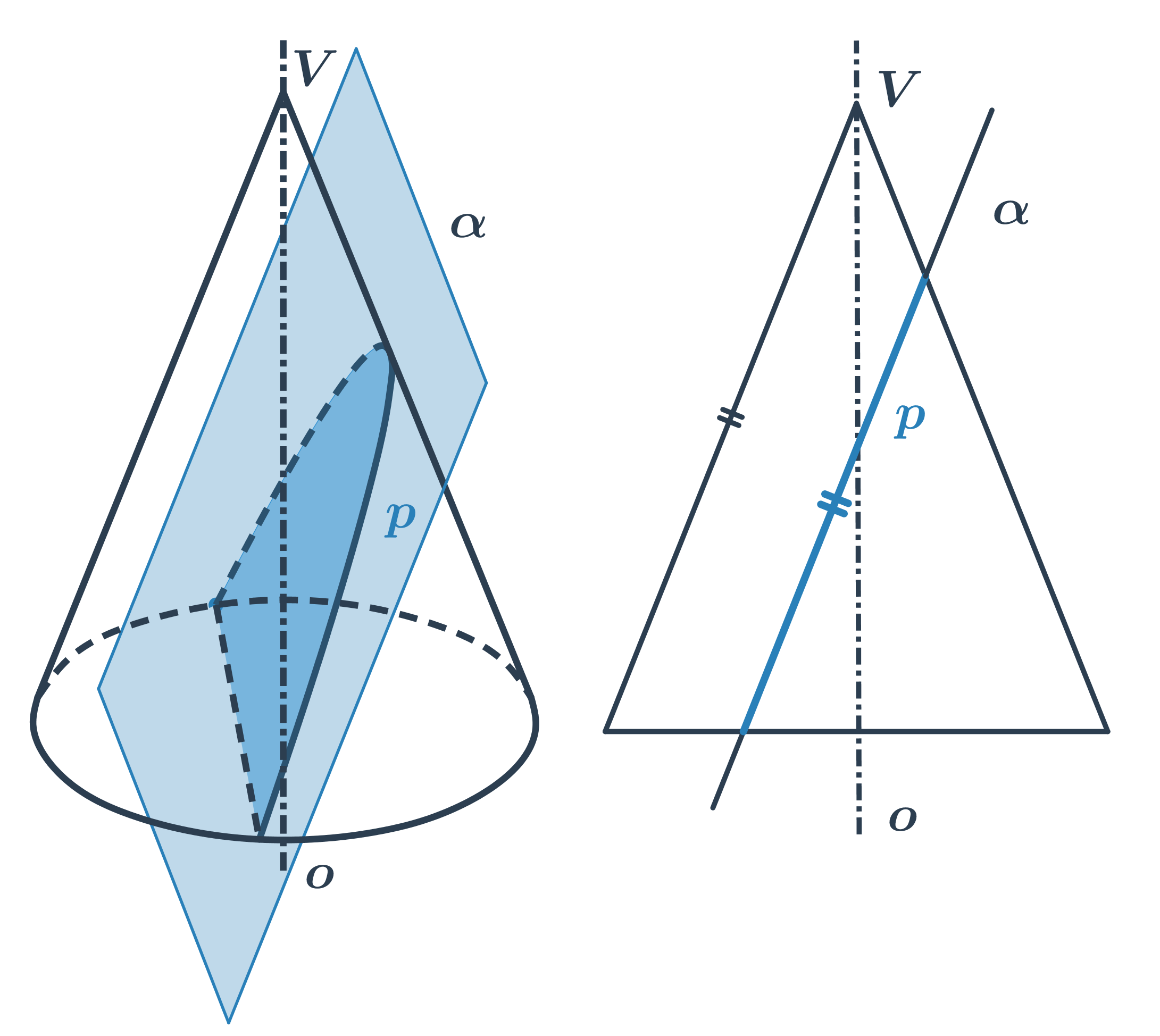
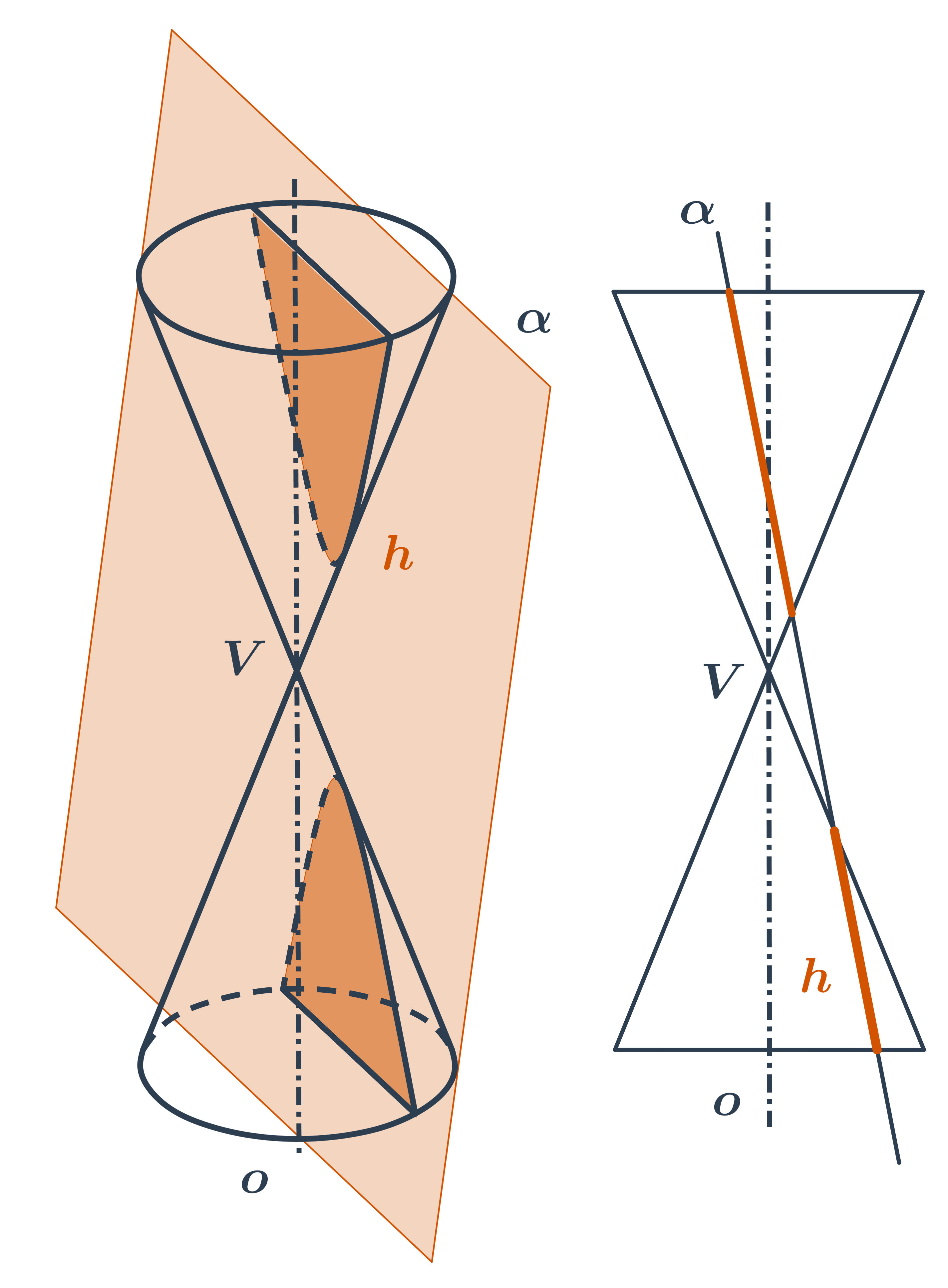
Na kuželosečky můžeme také hledět jako na množiny bodů dané vlastnosti. V analytické geometrii často zapisujeme tyto množiny pomocí rovnic.

Kružnice (kuželosečka)

Kružnice je množina všech bodů v rovině, které mají od daného pevného bodu S stejnou vzdálenost r. Bod S nazýváme střed kružnice, polohu r nazveme poloměr kružnice.

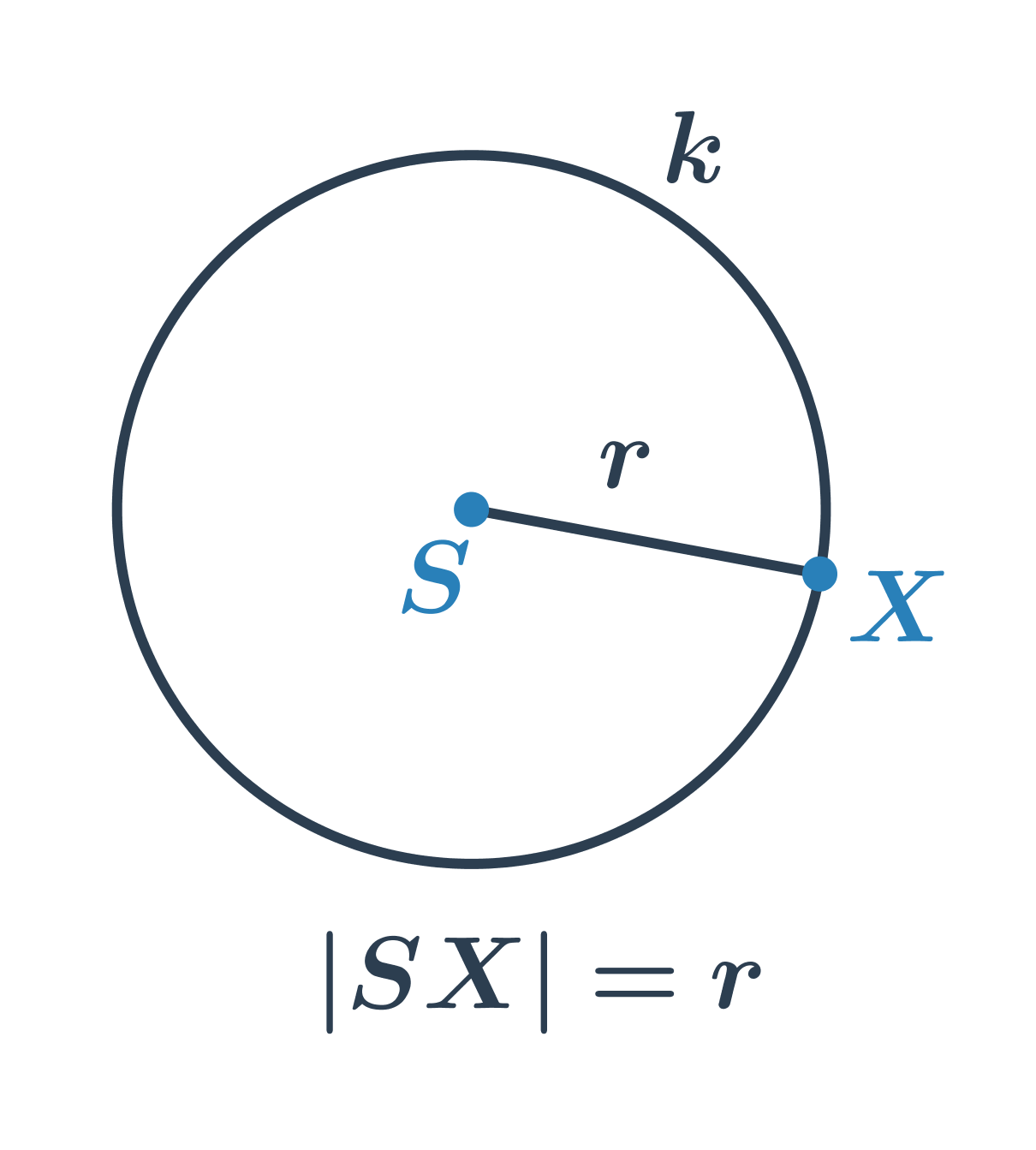
Středová rovnice kružnice

Středová rovnice kružnice o středu S[m;n] a poloměru r ve tvaru: (x - m)² + (y - n)² = r²

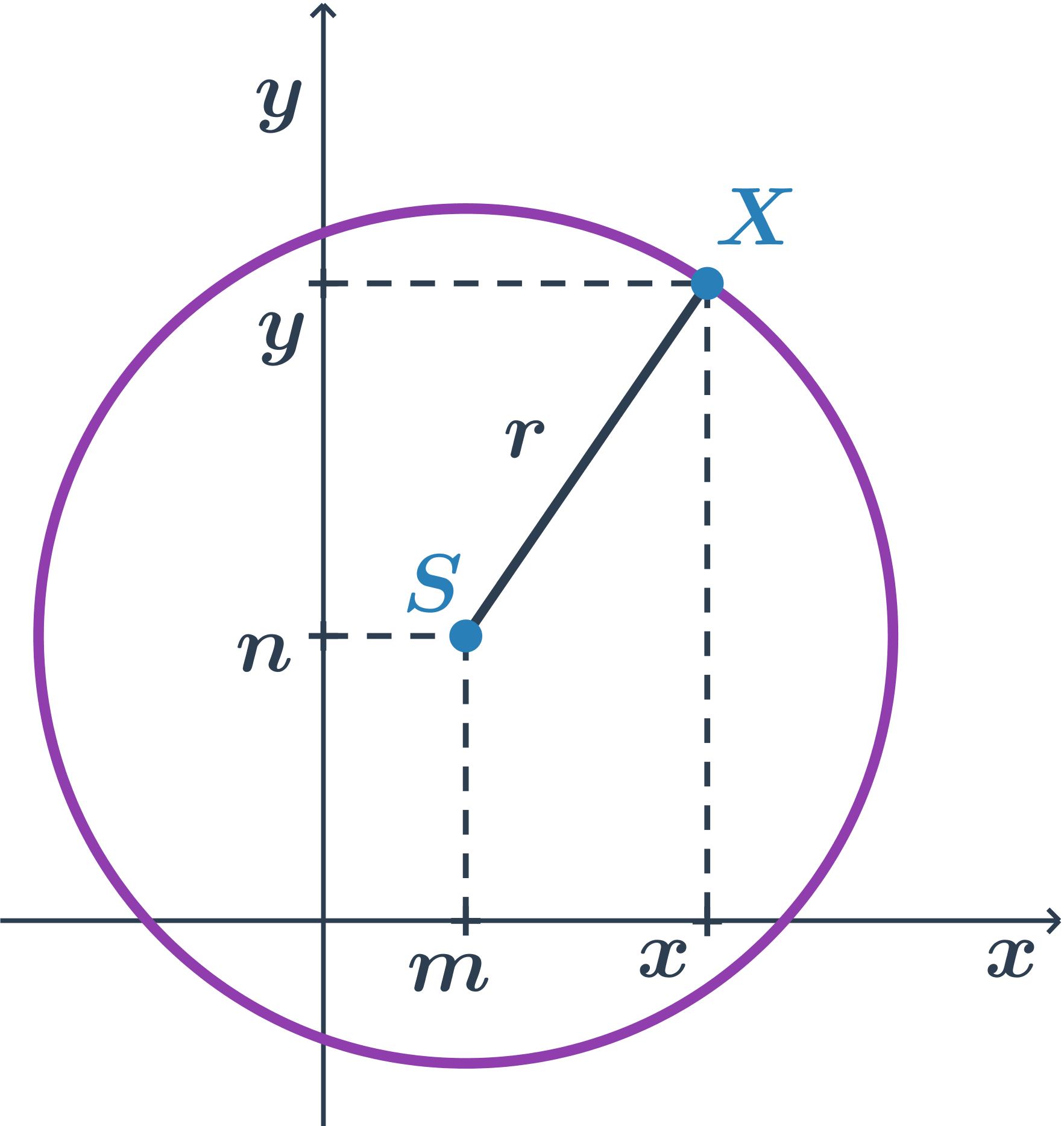
Obecná rovnice kružnice

Podobně jako existuje několik tvarů rovnic přímky, můžeme i rovnici kružnice zapsat různými způsoby. Obecná rovnice kružnice je ve tvaru: x² + y² - 2mx - 2ny + p = 0

Každá rovnice v tomto tvaru ale nemusí ještě být obecnou rovnicí kružnice. Pro obecnou rovnici kružnice musí platit, že výraz m² + n² - p je kladný. Praktické ověření, zda se jedná o kružnici, ale obvykle provádíme převedením na středovou rovnici kružnice.

Kružnice a přímka

přímka s protíná kružnici ve dvou bodech – sečna kružnice
přímka t protíná kružnici v jednom bodě – tečna kružnice
přímka v kružnici neprotíná – vnější přímka kružnice

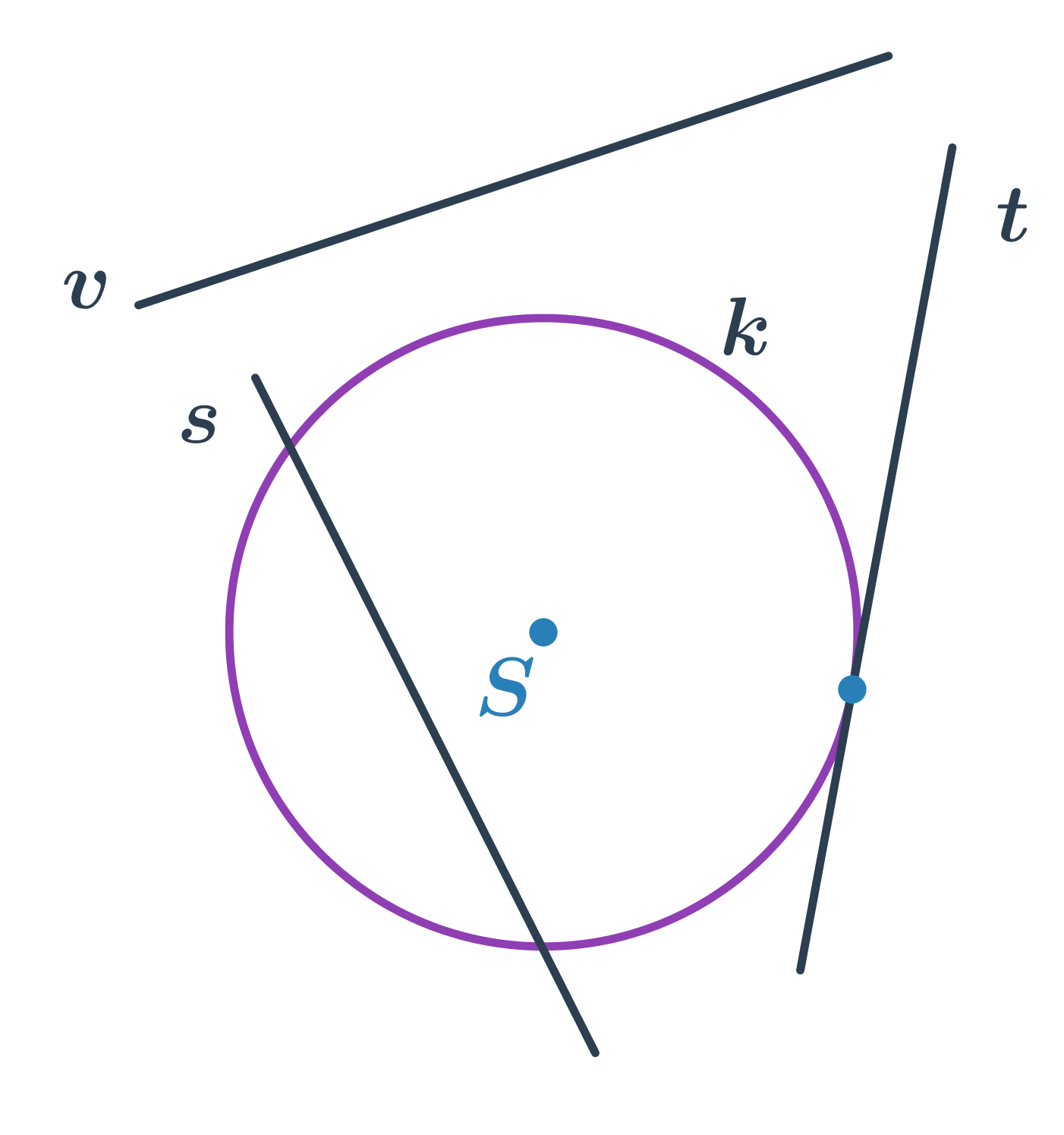
Rovnice tečny kružnice v bodě, který leží na kružnici

Kružnice daná rovnicí (x - m)² + (y - n)² = r² má v bodě T[x₀;y₀] tečnu (x₀ - m)(x - m) + (y₀ - n)(y - n) = r²

Polára kružnice

Z bodu R mimo kružnici můžeme sestrojit dvě tečny k dané kružnici. Přímka určená body dotyku tečen se nazývá polára kružnice vzhledem k bodu R.

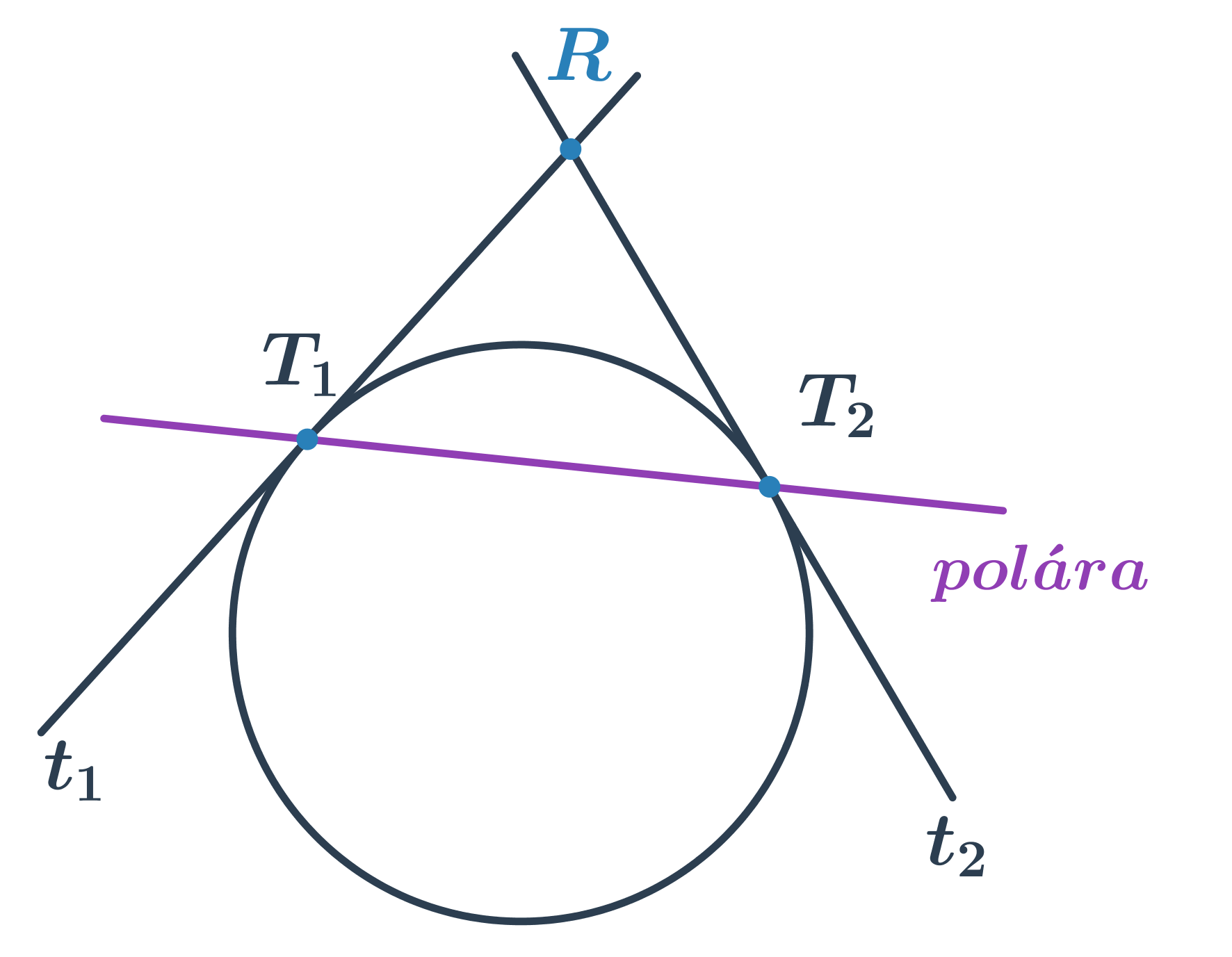
Rovnice poláry kružnice kružnice (x - m)² + (y - n)² = r² vzhledem k bodu R[r₁;r₂] je (r₁ - m)(x - m) + (r₂ - n)(y - n) = r².

Elipsa

Elipsa je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý součet vzdáleností 2a, který je větší než vzdálenost ohnisek.

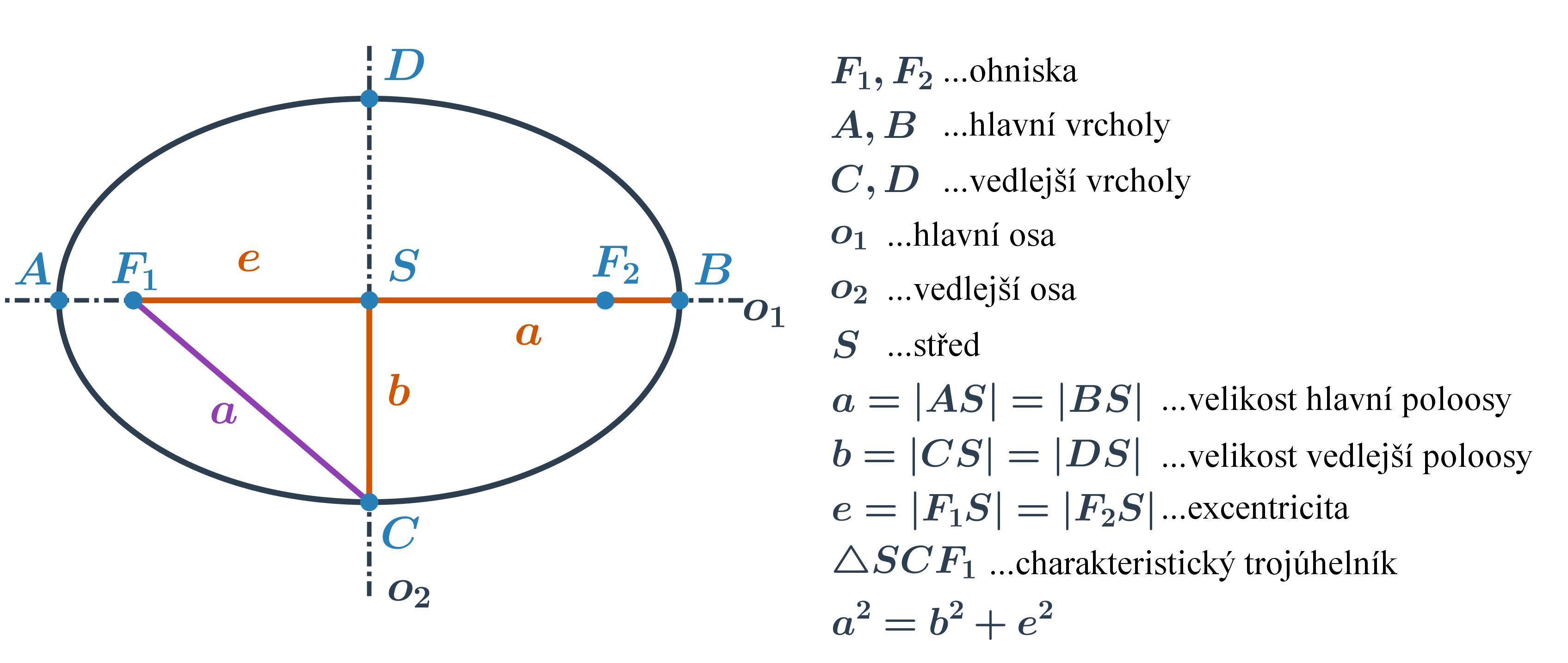
Středová rovnice elipsy

Tvar středové rovnice elipsy o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a a b závisí na poloze hlavní osy:

hlavní osa je rovnoběžná s osou x, rovnice je ve tvaru: $\frac{(x - m)²}{a²}$ + $\frac{(y - n)²}{b²}$ = 1

×
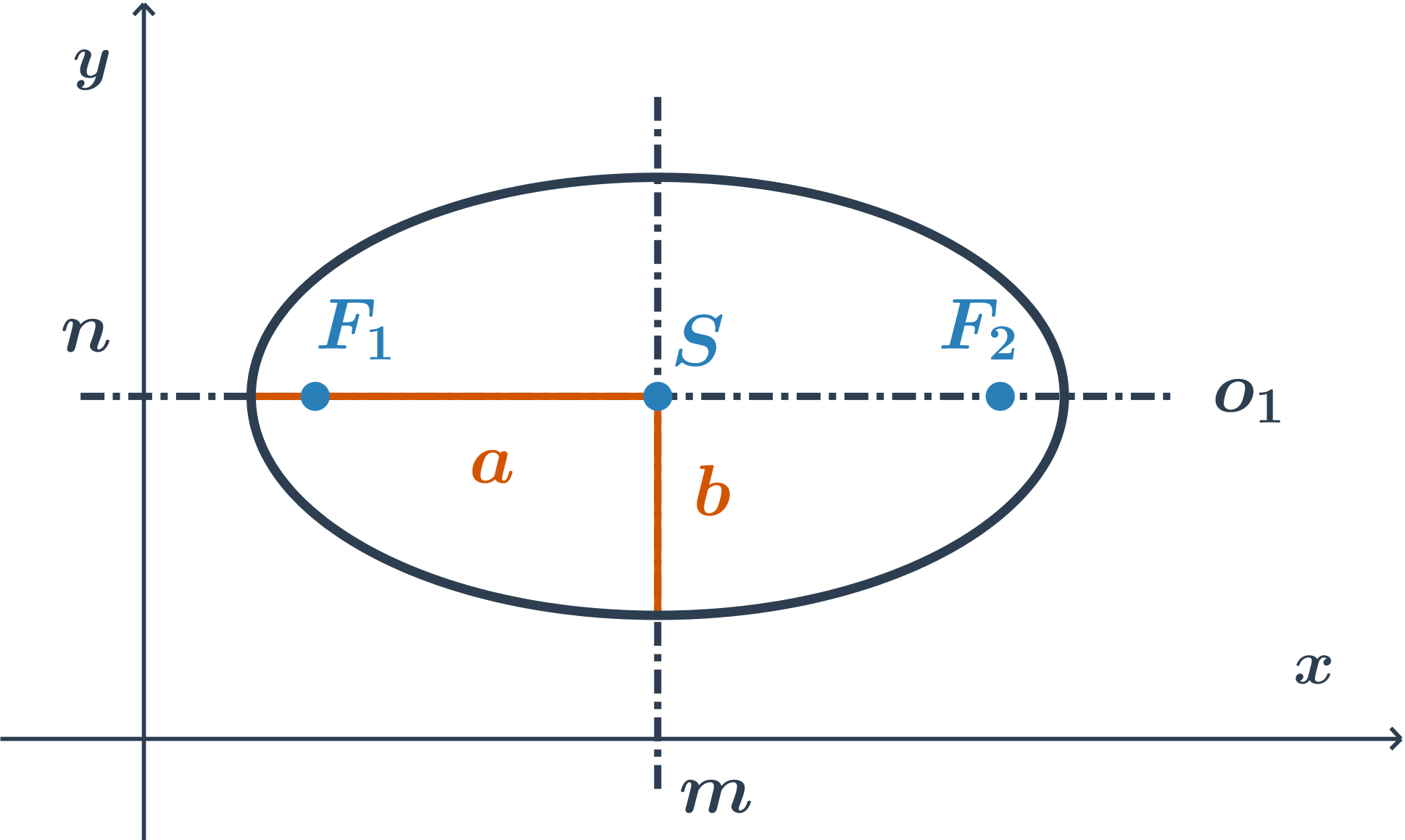hlavní osa je rovnoběžná s osouy, rovnice je ve tvaru: $\frac{(x - m)²}{b²}$ + $\frac{(y - n)²}{a²}$ = 1

×

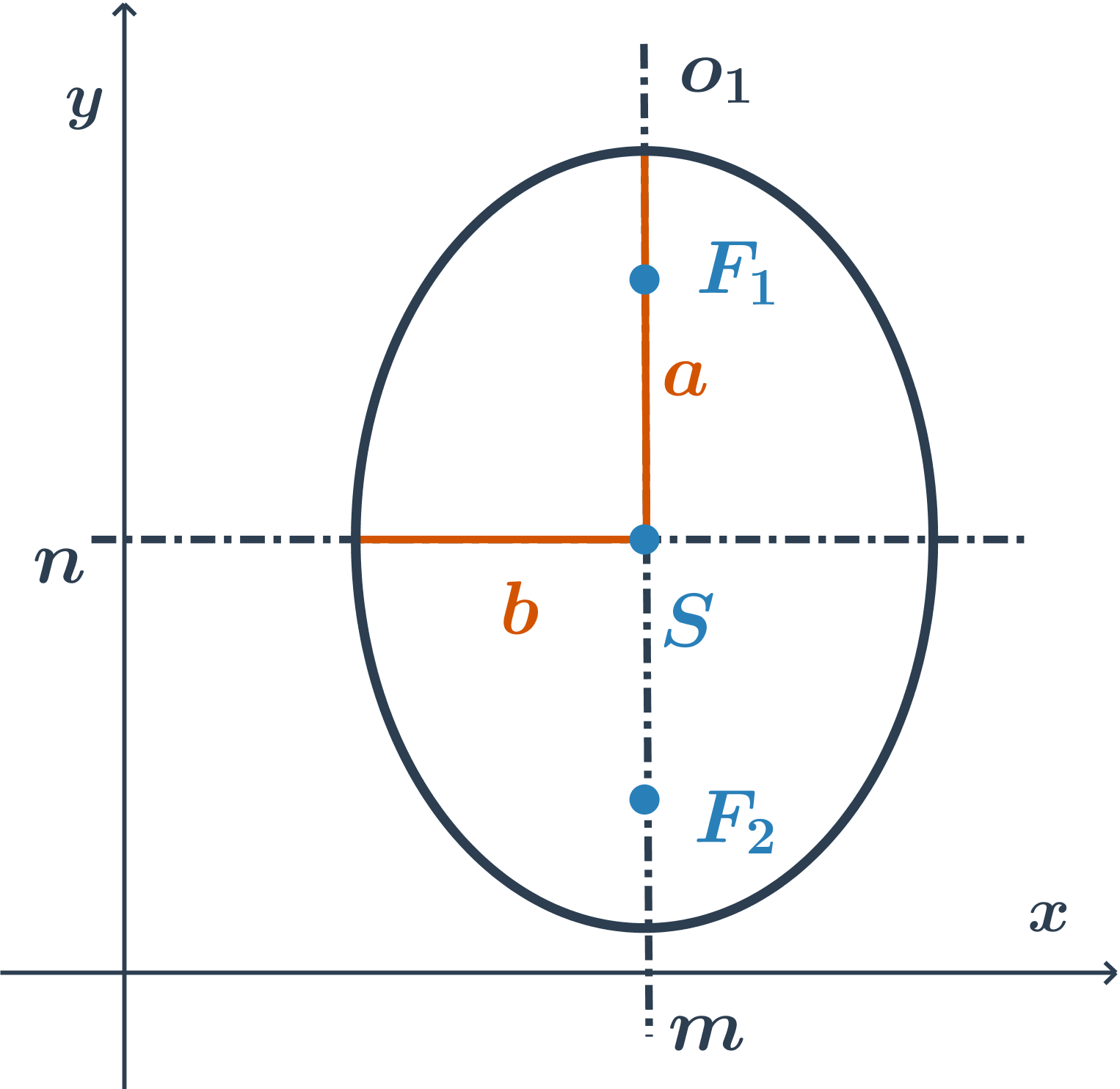Obecná rovnice elipsy

Podobně jako existuje několik rovnic přímky, můžeme i rovnici elipsy zapsat jiným způsobem. Obecná rovnice elipsy je ve tvaru:
Ax² + By² + Cx + Dy + E = 0,A ≠ B,A ⋅ B > 0.

Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí elipsy. Praktické ověření, zda se jedná o elipsu provádíme převedením na středovou rovnici.

Elipsa a přímka

přímka s protíná elipsu ve dvou bodech – sečna elipsy
přímka t protíná elipsu v jednom bodě – tečna elipsy
přímka v elipsu neprotíná – vnější přímka elipsy

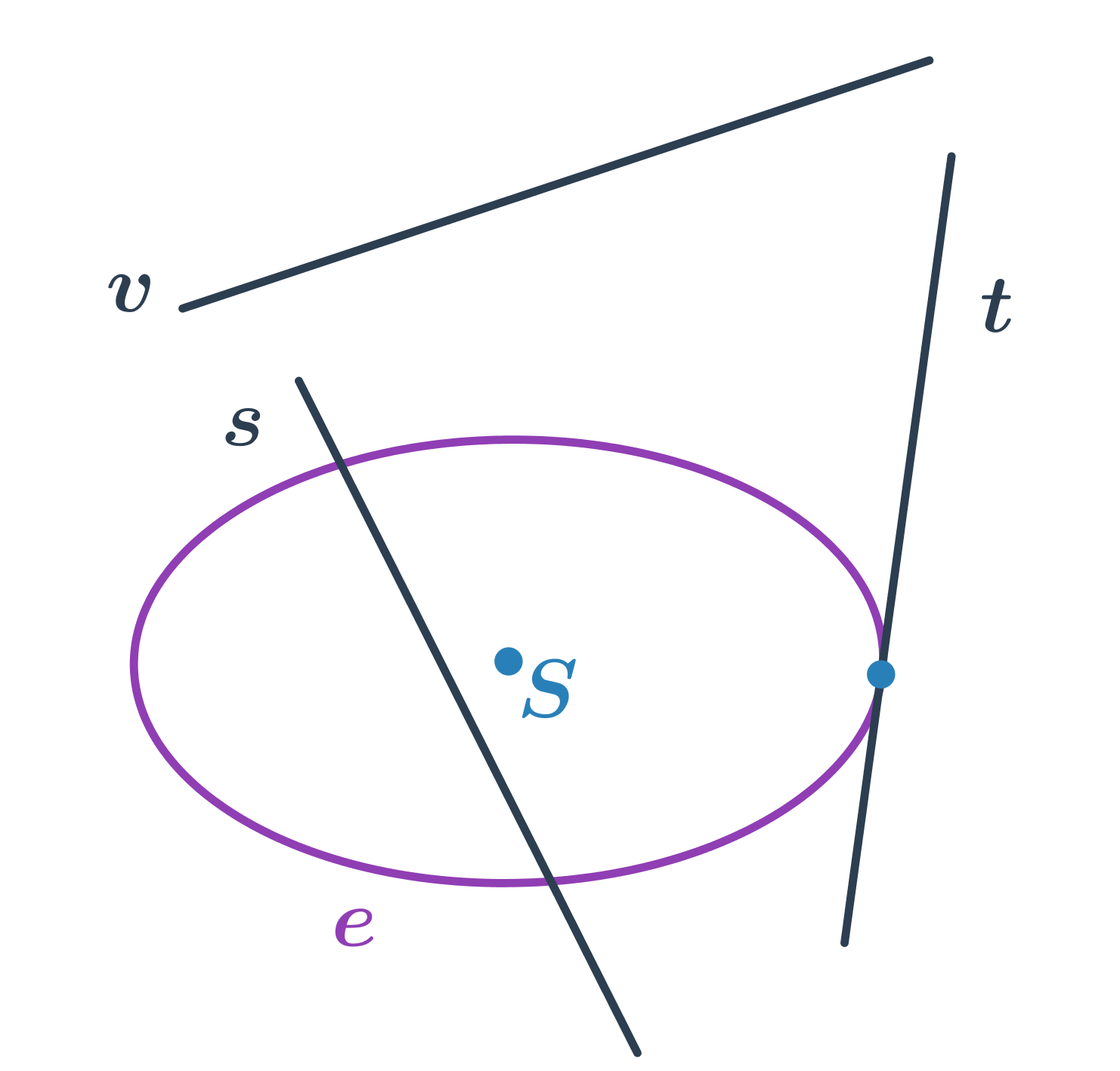
Rovnice tečny elipsy v bodě, který leží na elipse

Elipsa daná rovnicí $\frac{(x - m)²}{a²}$ + $\frac{(y - n)²}{b²}$ = 1 má v bodě T[x₀;y₀] tečnu určenou rovnicí: $\frac{(x - m)(x₀ - m)}{a²}$ + $\frac{(y - n)(y₀ - n)}{b²}$ = 1

Podobně můžeme zapsat i rovnici tečny elipsy, která má hlavní osu rovnoběžnou s osou y.

Parabola

Parabola je množina všech bodů roviny, které mají stejnou vzdálenost od daného bodu (ohnisko) a dané přímky (řídící přímka)

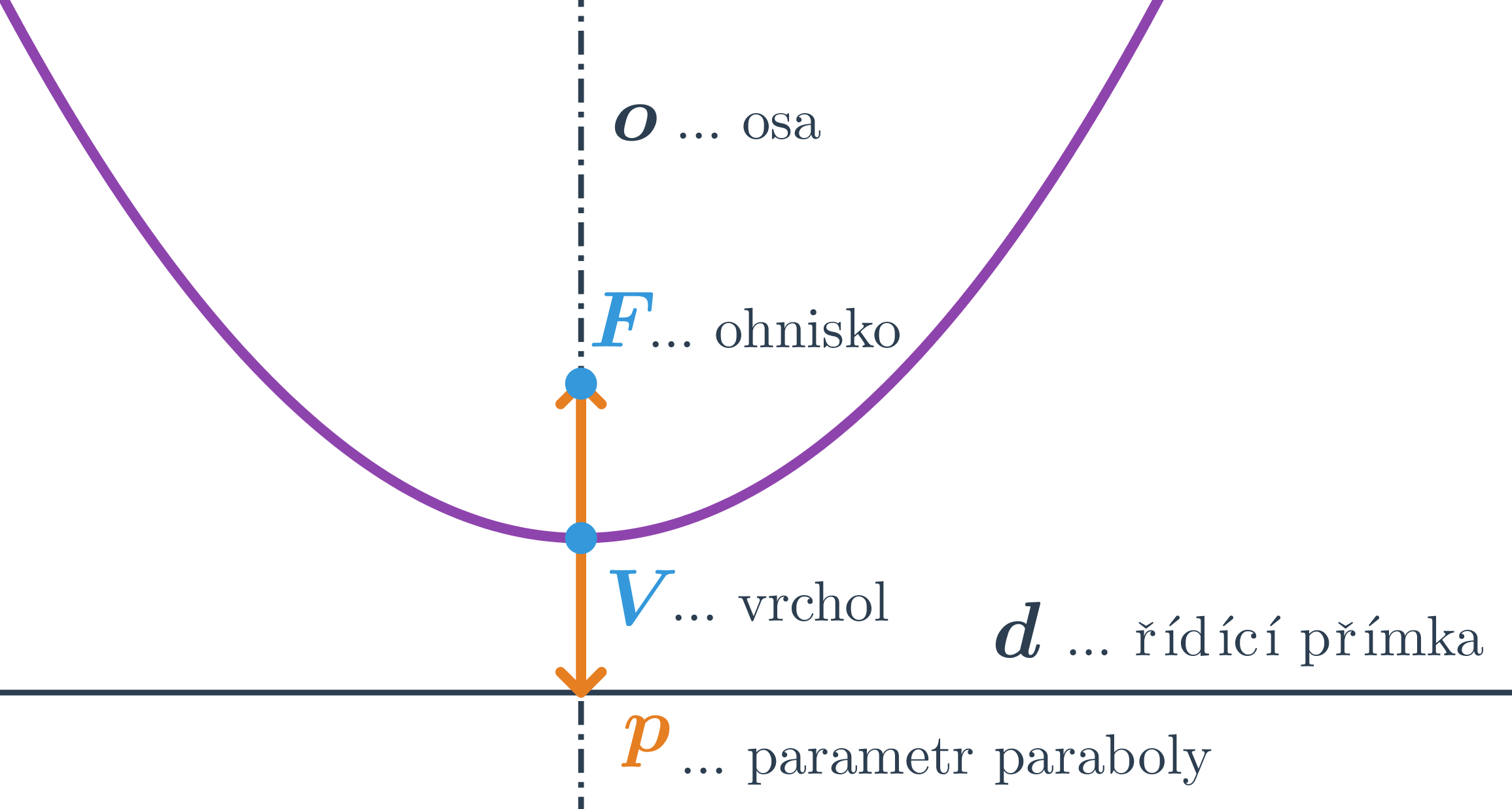
Vrcholová rovnice paraboly

Tvar rovnice závisí na umístění osy:

osa paraboly rovnoběžná s osou y, vrcholová rovnice pak má tvar: (x - m)² = ±2p(y - n)
osa paraboly rovnoběžná s osou x, vrcholová rovnice pak má tvar: (y - n)² = ±2p(x - m)

V rovnici paraboly označují m, n souřadnice vrcholu paraboly, tedy vrchol je bod V = [m;n]. Dále p, je parametr paraboly = vzdálenost ohniska od řídící přímky. Znaménko před parametrem závisí na poloze vrcholu vzhledem k bodům paraboly.

Obecná rovnice paraboly

Tvar rovnice závisí na umístění osy:

osa paraboly je rovnoběžná s osou y:y = ax² + bx + c
osa paraboly je rovnoběžná s osou x:x = ay² + by + c

Přímka a parabola

přímka b protíná parabolu ve dvou bodech – sečna paraboly
přímka a se dotýká paraboly v jednom bodě – tečna paraboly
přímka c neprotíná parabolu

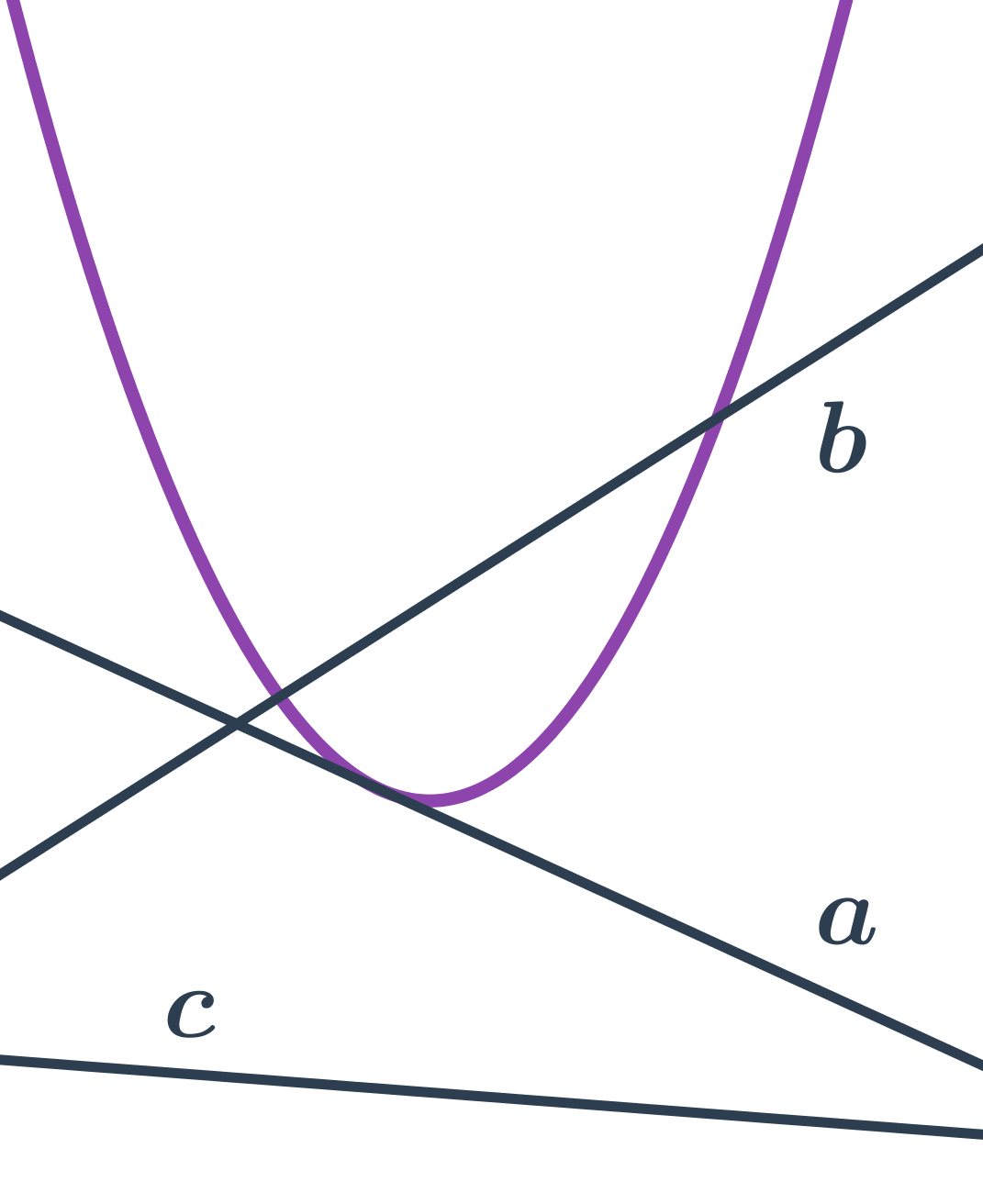
Rovnice tečny paraboly v bodě, který leží na parabole

parabola daná rovnicí (x - m)² = ±2p(y - n) má v bodě T = [x₀;y₀] tečnu danou rovnicí: (x₀ - m)(x - m) = ±p(y₀ - n) ±p(y - n)
parabola daná rovnicí (y - n)² = ±2p(x - m) má v bodě T = [x₀;y₀] tečnu danou rovnicí: (y₀ - n)(y - n) = ±p(x₀ - m) ±p(x - m)

Hyperbola

Hyperbola je množina všech bodů v rovině, které mají od dvou různých bodů (ohnisek) stálý rozdíl vzdáleností 2a, který je menší než vzdálenost ohnisek. Hyperbola se skládá ze dvou částí – větví hyperboly. Tyto dvě větve se blíží k přímkám, které nazýváme asymptoty.

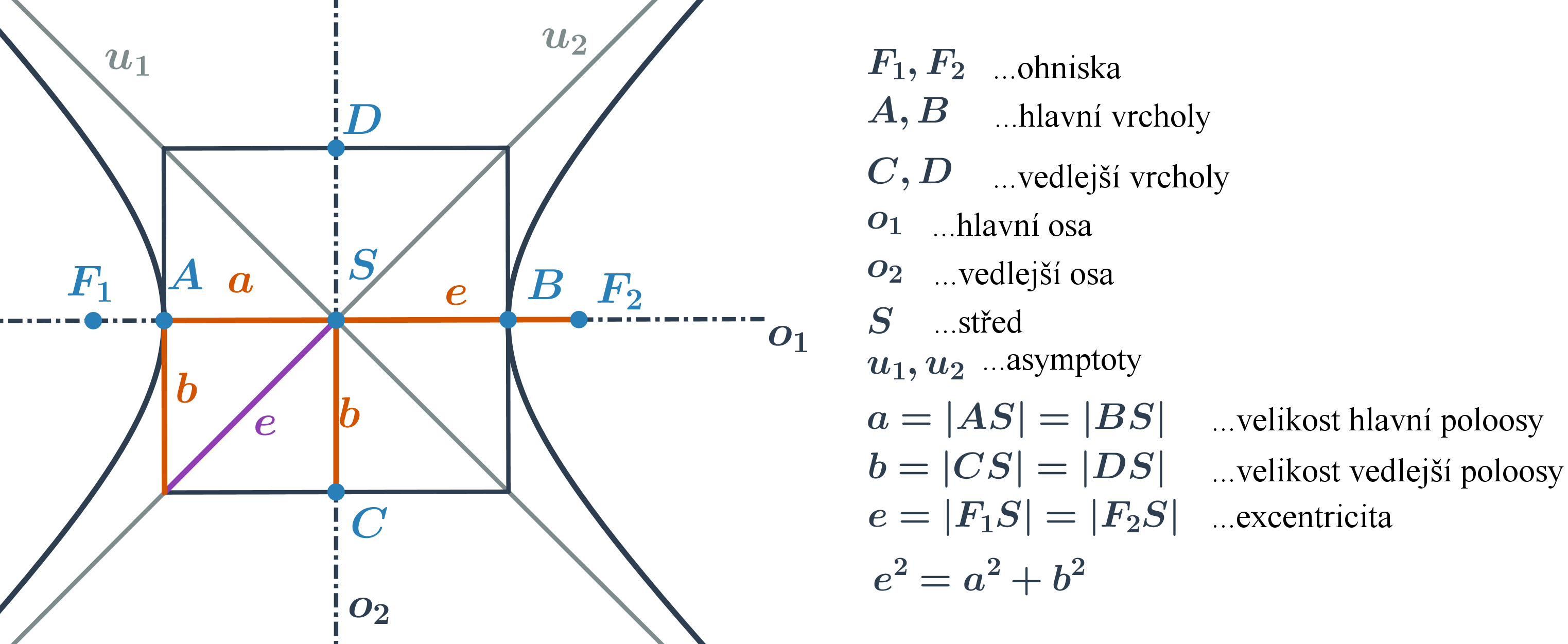
Středová rovnice hyperboly

Tvar středové rovnice hyperboly o středu S[m;n] s velikostmi hlavní a vedlejší poloosy a, b závisí na poloze hlavní osy.

Na rozdíl od elipsy, nemusí být u hyperboly vždy hlavní poloosa a delší než vedlejší poloosa b. Pro rovnoosou hyperbolu dokonce platí a = b.

Rovnice asymptot

Už víme, že asymptoty jsou přímky, ke kterým se hyperbola blíží. Pomohou při vykreslení hyperboly. Rovnice asymptot závisí na tvaru středové rovnice hyperboly.

Pro hyperbolu danou rovnicí ve tvaru $\frac{(x - m)²}{a²}$ - $\frac{(y - n)²}{b²}$ = 1 jsou rovnice asymptot: y = ± $\frac{b}{a}$ (x - m) + n

Pro hyperbolu danou rovnicí ve tvaru - $\frac{(x - m)²}{b²}$ + $\frac{(y - n)²}{a²}$ = 1 jsou rovnice asymptot: y = ± $\frac{a}{b}$ (x - m) + n

Obecná rovnice hyperboly

Podobně jako existuje několik rovnic elipsy, můžeme i rovnici hyperboly zapsat různými způsoby. Obecná rovnice hyperboly je ve tvaru: Ax² + By² + Cx + Dy + E = 0,A ⋅ B < 0. Podmínka A ⋅ B < 0 zaručuje, že konstanty A, B mají opačná znaménka. Každá rovnice v tomto tvaru ale nemusí být obecnou rovnicí hyperboly. Praktické ověření, zda se jedná o hyperbolu provádíme převedením na středovou rovnici.

Hyperbola a přímka

přímka s protíná hyperbolu ve dvou bodech – sečna hyperboly
přímka t protíná hyperbolu v jednom bodě – tečna hyperboly
přímka v hyperbolu neprotíná – vnější přímka hyperboly

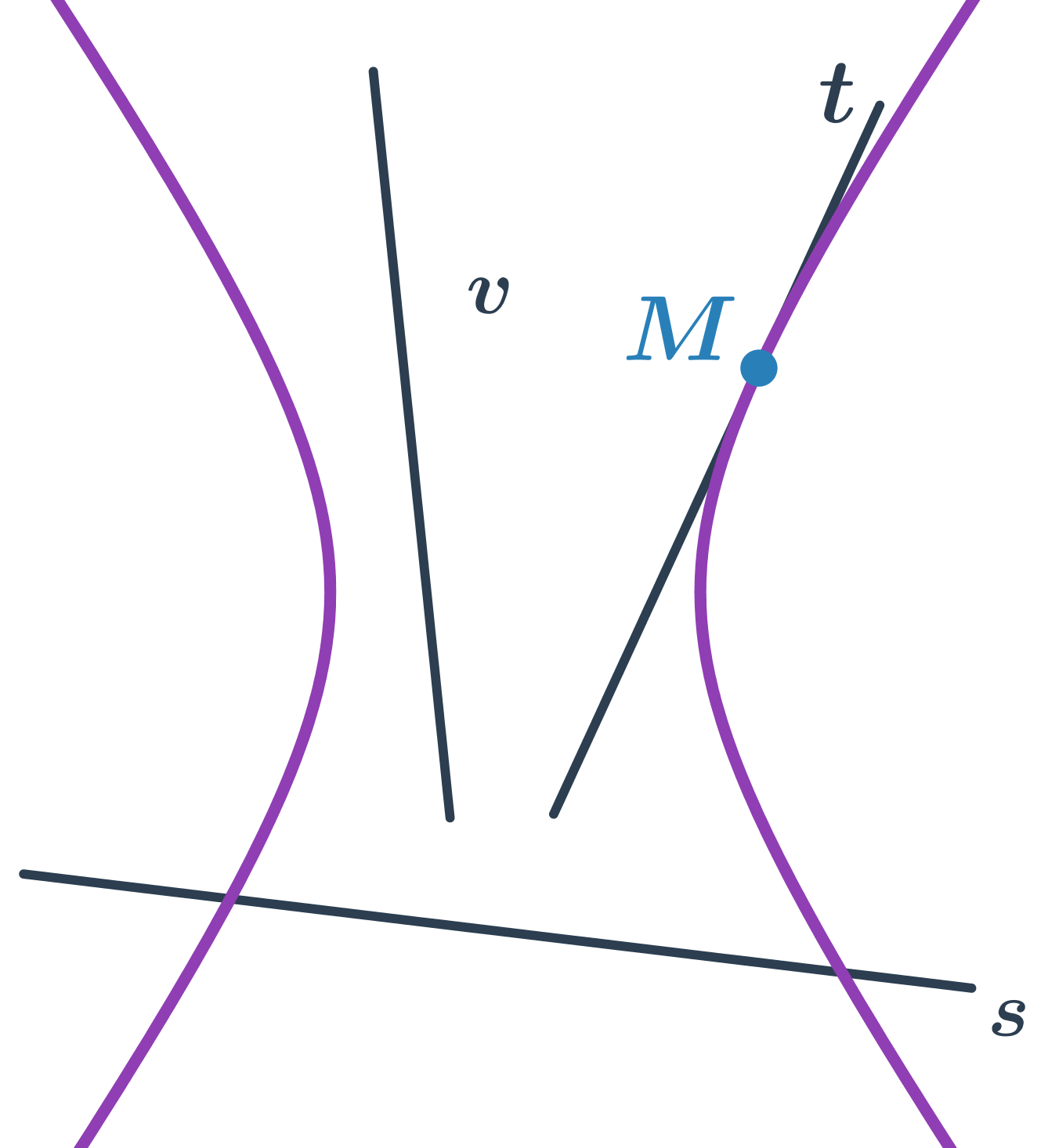
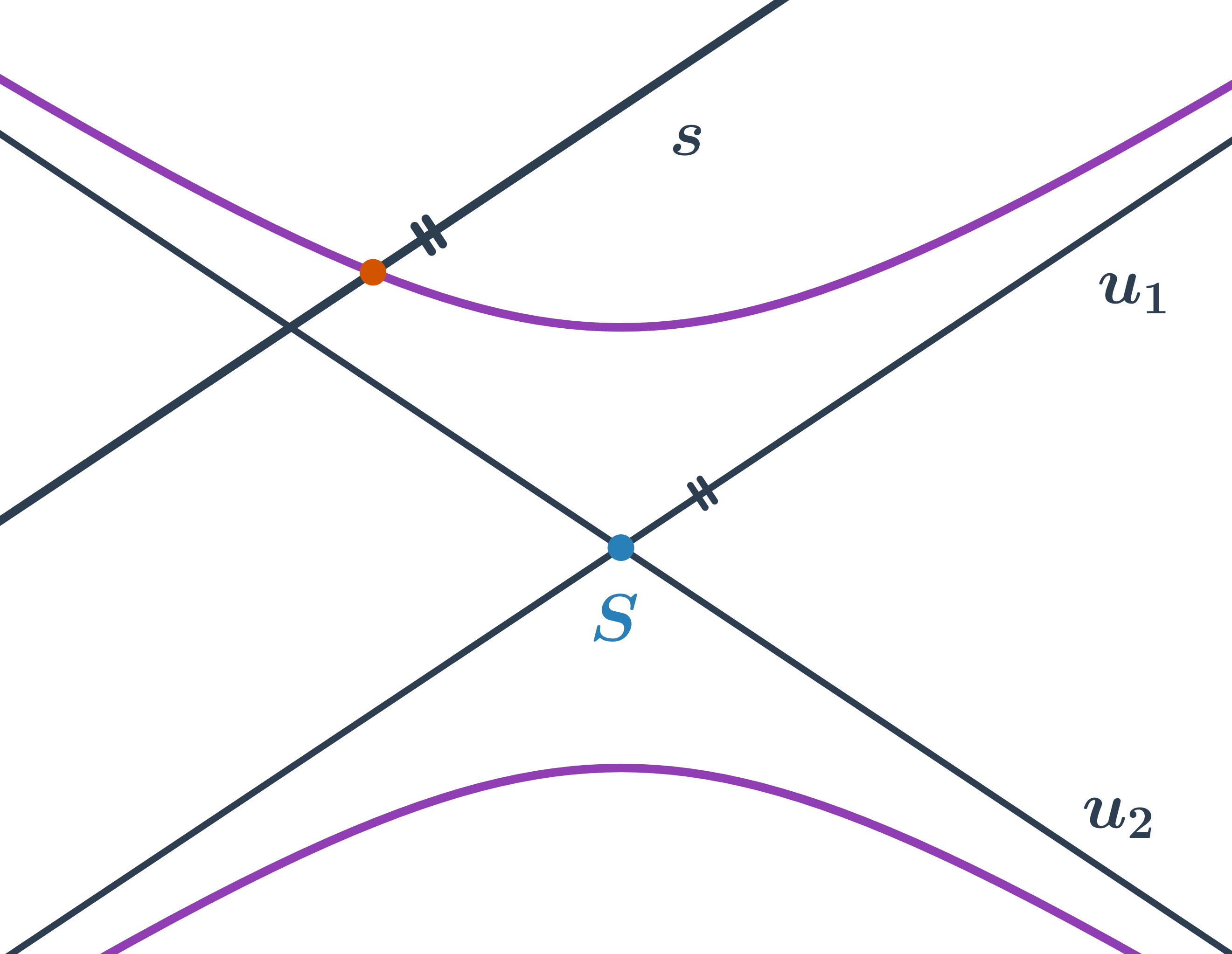
Speciální polohou sečny hyperboly je přímka, která je rovnoběžná s asymptotou. Taková sečna pak protíná hyperbolu v jednom bodě.

Rovnice tečny hyperboly v bodě, který leží na hyperbole

Hyperbola daná rovnicí $\frac{(x - m)²}{a²}$ - $\frac{(y - n)²}{b²}$ = 1 má v bodě T[x₀;y₀] tečnu danou rovnicí: $\frac{(x - m)(x₀ - m)}{a²}$ - $\frac{(y - n)(y₀ - n)}{b²}$ = 1

Podobně můžeme zapsat i rovnici tečny hyperboly, která má hlavní osu rovnoběžnou s osou y.