Graf funkce
V matematice je graf funkce f(x₁, x₂, x₃, ..., xn množina všech (n+1)-tic (x₁, x₂, ..., xn, f(x₁, x₂, ..., xn). Jako graf je též označena grafická reprezentace této množiny ve formě křivky, přímky, lomené čáry nebo plochy, spolu s osami v kartézské soustavě souřadnic.
Osa s nezávisle proměnnou (obvykle osa x) se označuje jako x-ová souřadnice nebo abscisa. Osa se závisle proměnnou (obvykle osa y) se označuje jako y-ová souřadnice, pořadnice nebo ordináta.
Graf nejčastěji zobrazuje závislost y=f(x), popř. z=f(x,y). V případě většího počtu nezávislých proměnných se obvykle používá graf zachycující závislost pouze na vybraných (jedné nebo dvou) proměnných.
Příklad
Graf funkce
je množina {(1,a), (2,d), (3,c)}.
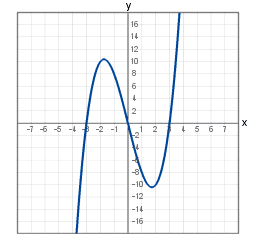
Graf polynomu třetího stupně na reálných číslech
f(x) = x³ - 9x
je {(x, x³ -9x), kde x je libovolné reálné číslo}. Graf zobrazený v kartézské soustavě souřadnic vypadá následovně: