Geometrické konstrukce
Konstrukční úlohou rozumíme úlohu, ve které chceme sestrojit určitý geometrický útvar (alespoň jeden, případně všechny) splňující dané podmínky. Jinými slovy, pomocí pravítka, kružítka a případně i úhloměru sestrojíme geometrický útvar (trojúhelník, obdélník atd.), pro který známe délky jeho stran, velikosti úhlů či jiné vlastnosti.
Před rýsováním je dobré si ujasnit:
- body značíme velkými písmeny, např bod A
- přímky značíme malými písmeny, např. přímka p
Obvyklé kroky řešení konstrukční úlohy
Náčrtek: Od ruky si nakreslíme obrázek hledaného útvaru se vším, co známe ze zadání. To nám pomůže představit si výsledek. Pro přehlednost můžeme jednotlivé prvky vyznačit barevně. Nezapomeňte, náčrtky děláme velké a přehledné. V obrázku velkém jako blecha nic neuvidíme.
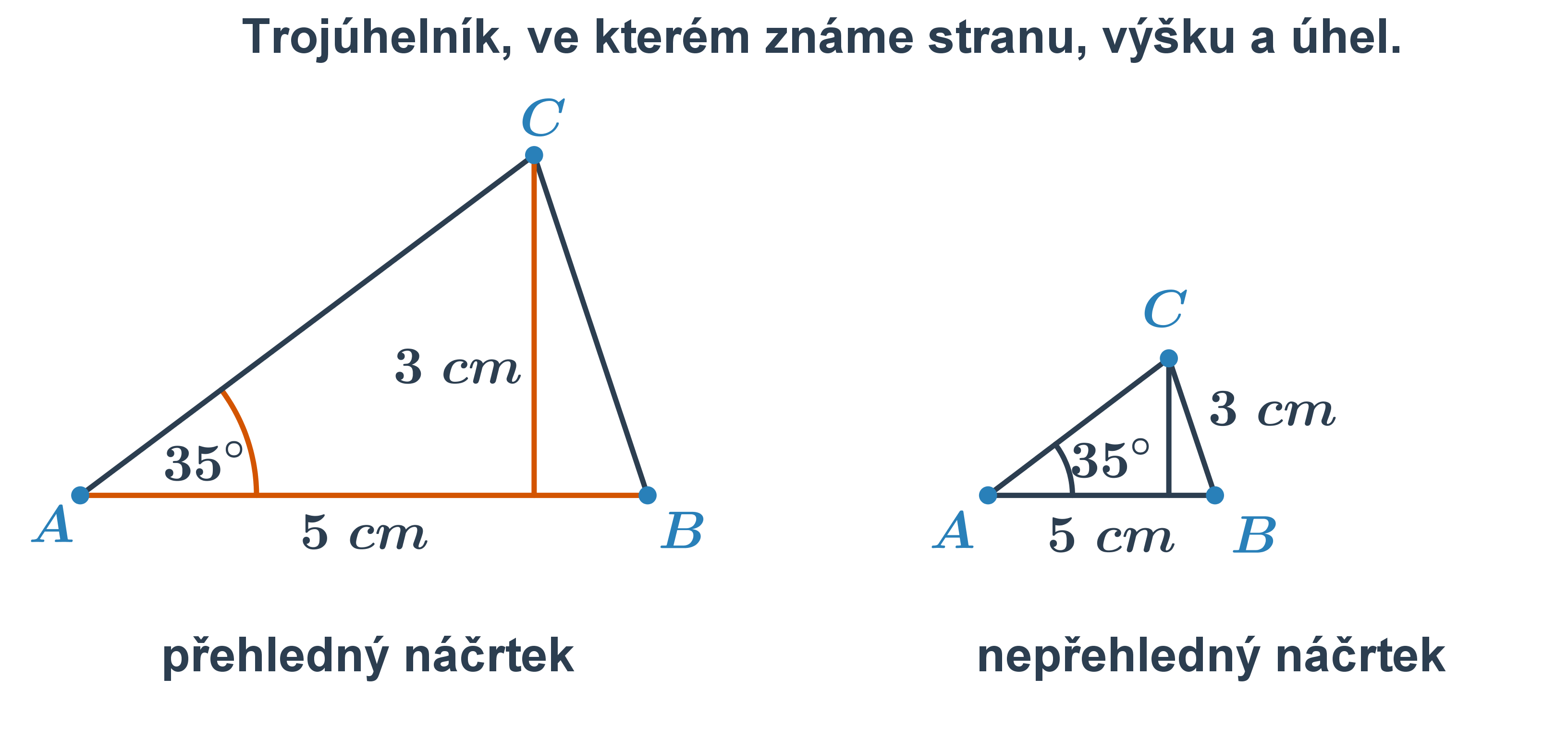
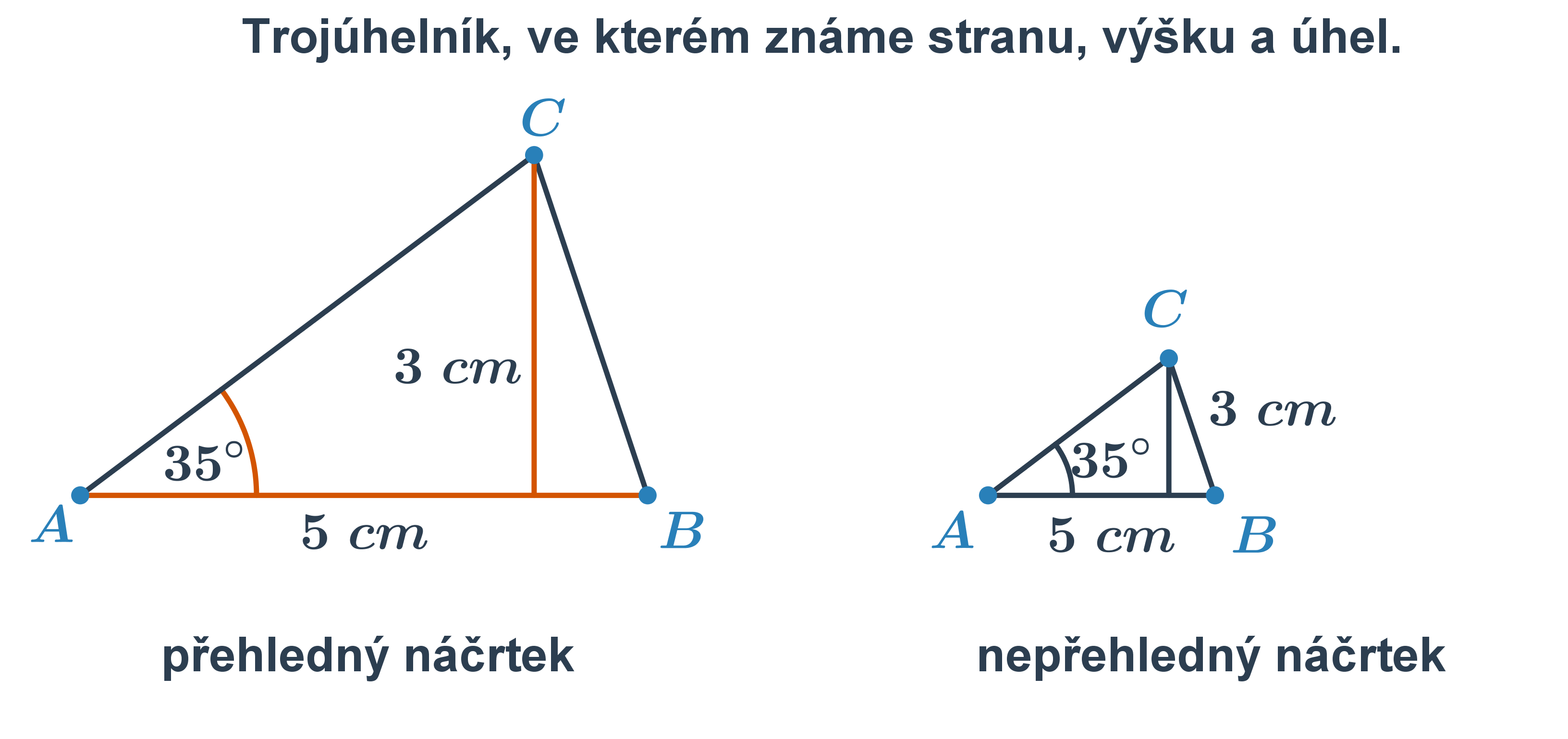
Trojúhelník, ve kterém známe stranu, výšku a úhel
konstrukce: Jde o samotné rýsování příkladu.
Zkouška správnosti: Měli bychom ověřit, jestli obrázek opravdu splňuje všechny podmínky ze zadání.
Počet řešení (diskuse): Zjistíme počet výsledků, které vyhovují zadání úlohy. Ne vždy musíme všechny výsledky narýsovat.
Geometrické konstrukce: značení
| Značka | Význam |
|---|---|
| p ∥ q | rovnoběžné přímky |
| p ⊥ q | Kolmé přímky |
| ∢ BAC | Úhel při vrcholu a |
| △ ABC | Trojúhelník ABC |
| ∣AB∣ | Délka úsečky AB |
| A ∈ p | A leží na přímce p |
| A∈/p | A neleží na přimce p |
| ↔ AB | Přímka procházející body A a B |
| ↦ AB | Polopřímka začínajici v bodě A, prochazející bodem B |
| ↦ ABC | polorovina s hraniční přímkou AB, obsahující bod C |
| ↦ pK | polorovina s hraniční přímkou p, obsahující bod K |
| ↔ ABC | Rovina určená body A, B a C |
| (p,q) | pás roviny, ohraničený rovnoběžkami p, q |
Dále využíváme pro zápis geometrických konstrukcí množinové operace, především průnik (∩) a sjednocení (∪)
Polopřímky a poloroviny
Polopřímka je část přímky, která vznikne rozdělením přímky jedním jejím bodem. Tento bod se nazývá počáteční. Polopřímku s počátečním bodem A procházející bodem B značíme ↦ AB. Každý bod rozděluje přímku na dvě opačné polopřímky se společným počátečním bodem.
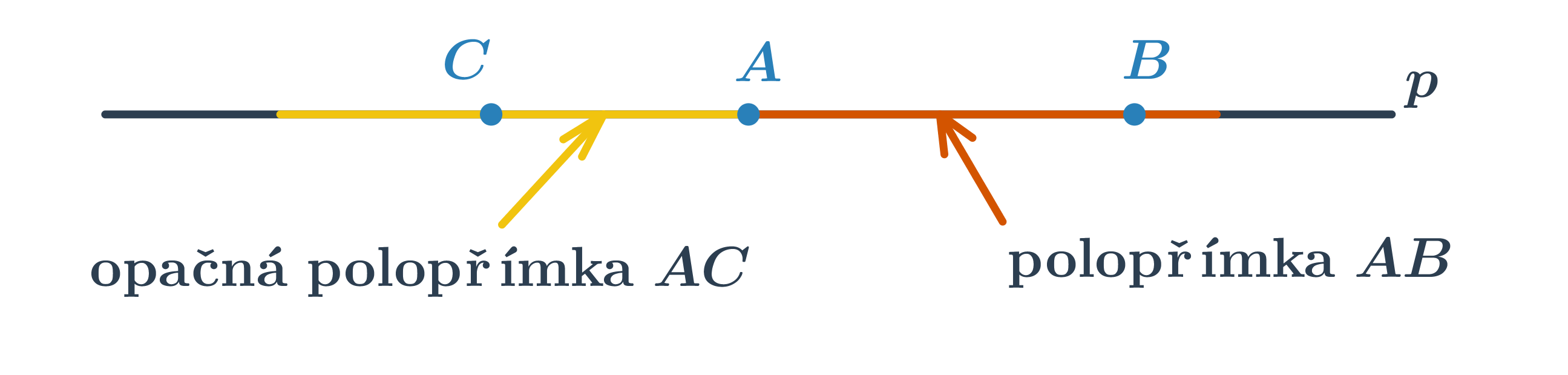
Základní vlastnosti polopřímek:
- Sjednocením dvou opačných polopřímek je přímka.
- Průnikem dvou opačných polopřímek je bod.
- Průnikem polopřímek ↦ AB a ↦ BA je úsečka AB
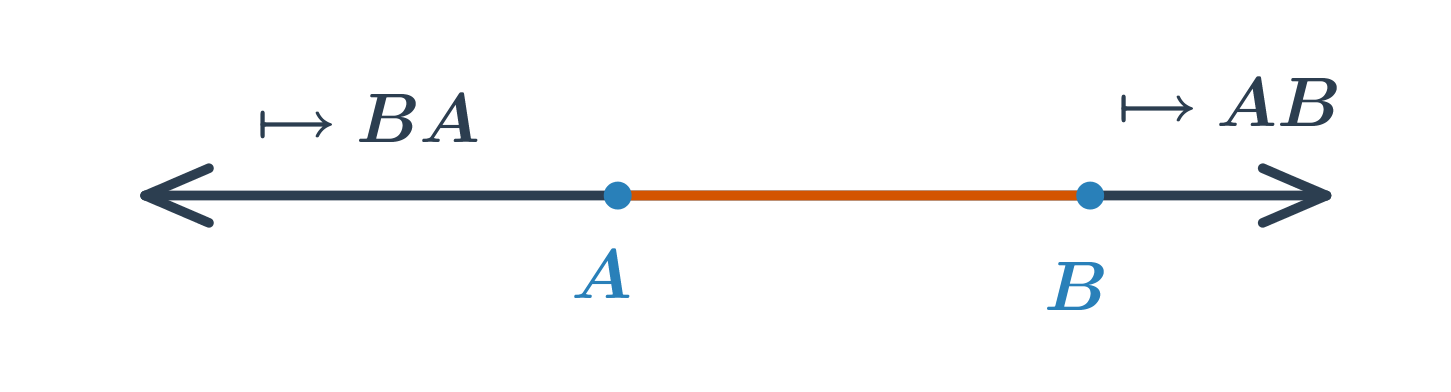
Polorovina je část roviny, která vznikne rozdělením roviny jednou přímkou. Tato přímka se nazývá hraniční. Polorovinu s hraniční přímkou p procházející bodem K značíme ↦ pK. Je-li přímka p určena body A, B, můzeme také psát ↦ ABK. Každá přímka rozděluje rovinu na dvě opačné poloroviny se společnou hraniční přímkou.
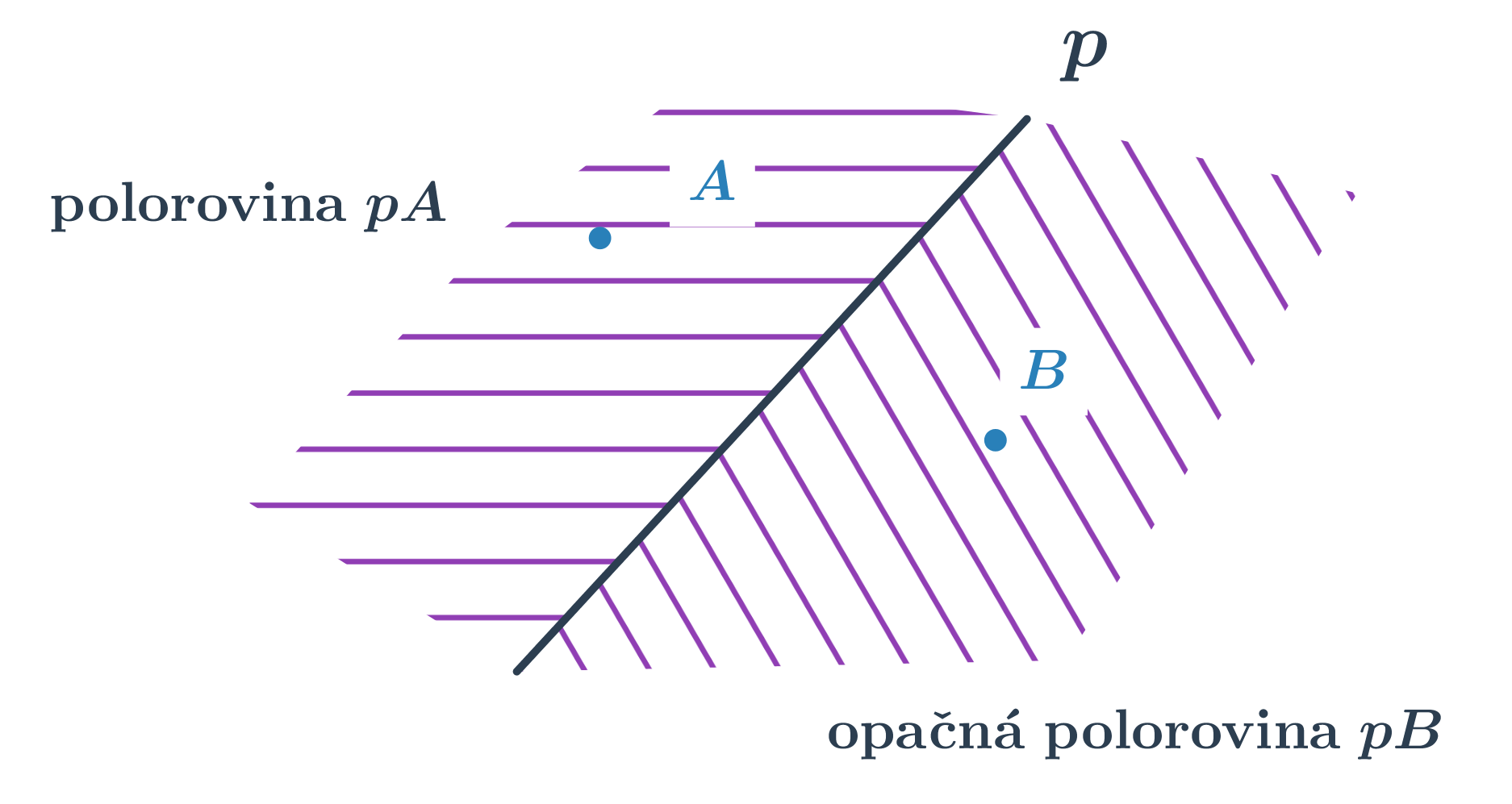
Základní vlastnosti polorovin:
- Sjednocením dvou opačných polorovin je rovina.
- Průnikem dvou opačných polorovin je hraniční přímka.
- Průnikem dvou polorovin s rovnoběžnými hraničními přímkami je pás rovnoběžek.
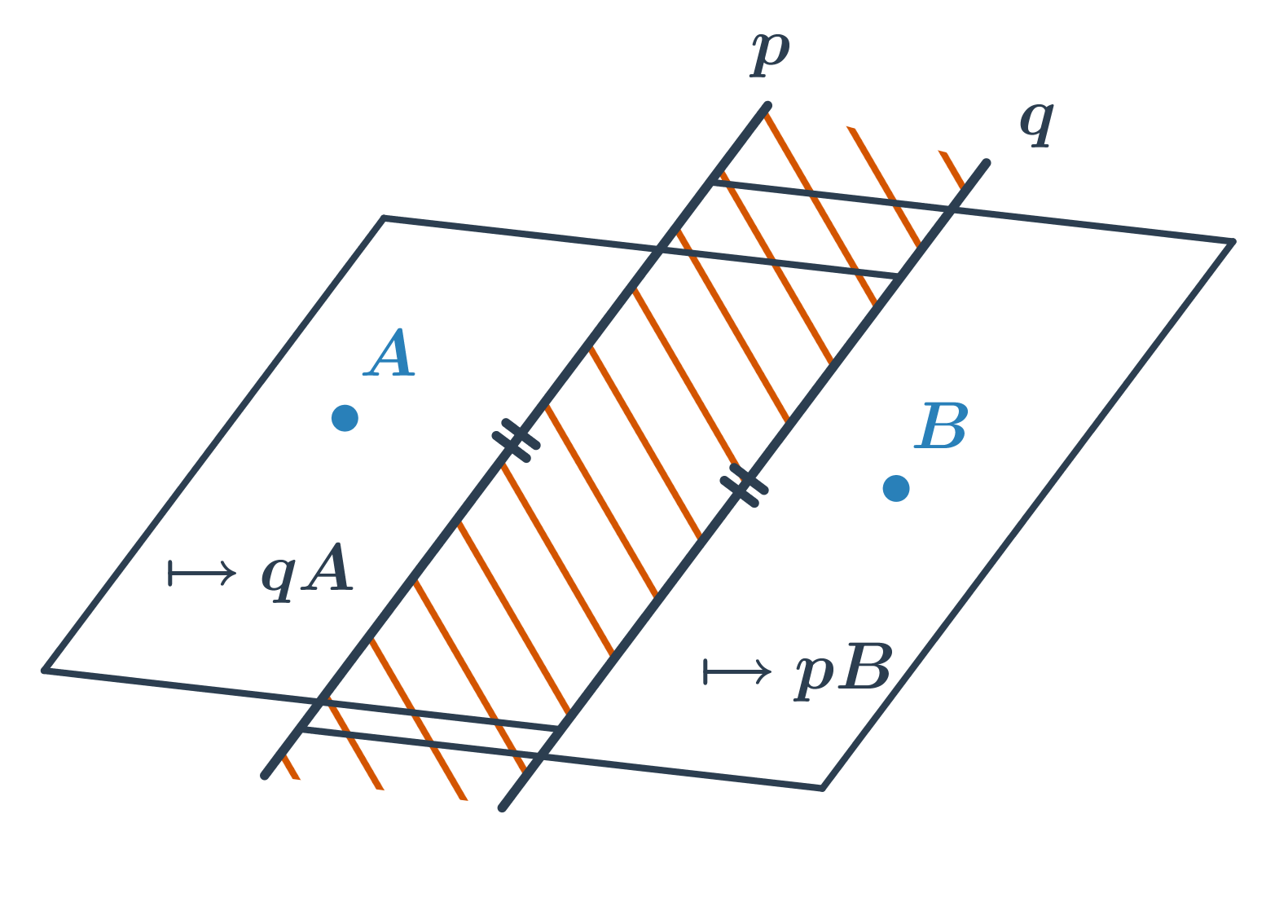
Pro zápis geometrických konstrukcí používáme množinové operace, především průnik ∩ a sjednocení ∪.
Rovnoběžky a kolmice
Rovnoběžky jsou dvě přímky ležící ve stejné rovině, které se nikde neprotínají. Rovnoběžnost přímek p a q zapisujeme p || q.
Kolmice je přímka, která protíná jinou přímku a svírá s ní úhel 90°. Kolmost přímek p a q zapisujeme p ⊥ q
Dvě přímky, které jsou kolmé na nějakou třetí přímku a současně obě leží v jedné rovině, jsou rovnoběžky.
Konstrukční úlohy: trojúhelníky
Při řešení jednodušších úloh provádíme konstrukce trojúhelníků se známými délkami stran. Nesmíme přitom zapomínat, že platí tzv. trojúhelníková nerovnost, tedy že součet dvou stran je větší než třetí strana. Jednoduše řečeno, jedině pokud je součet dvou nejkratších stran větší než třetí strana, trojúhelník lze sestrojit.
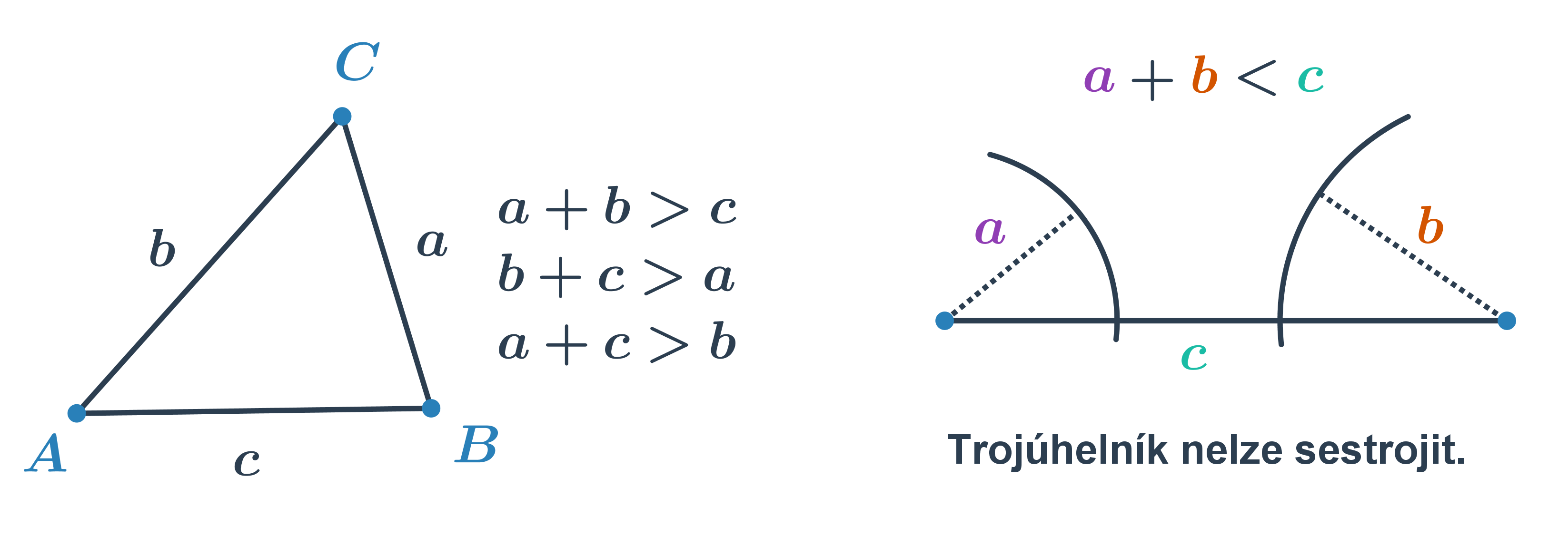
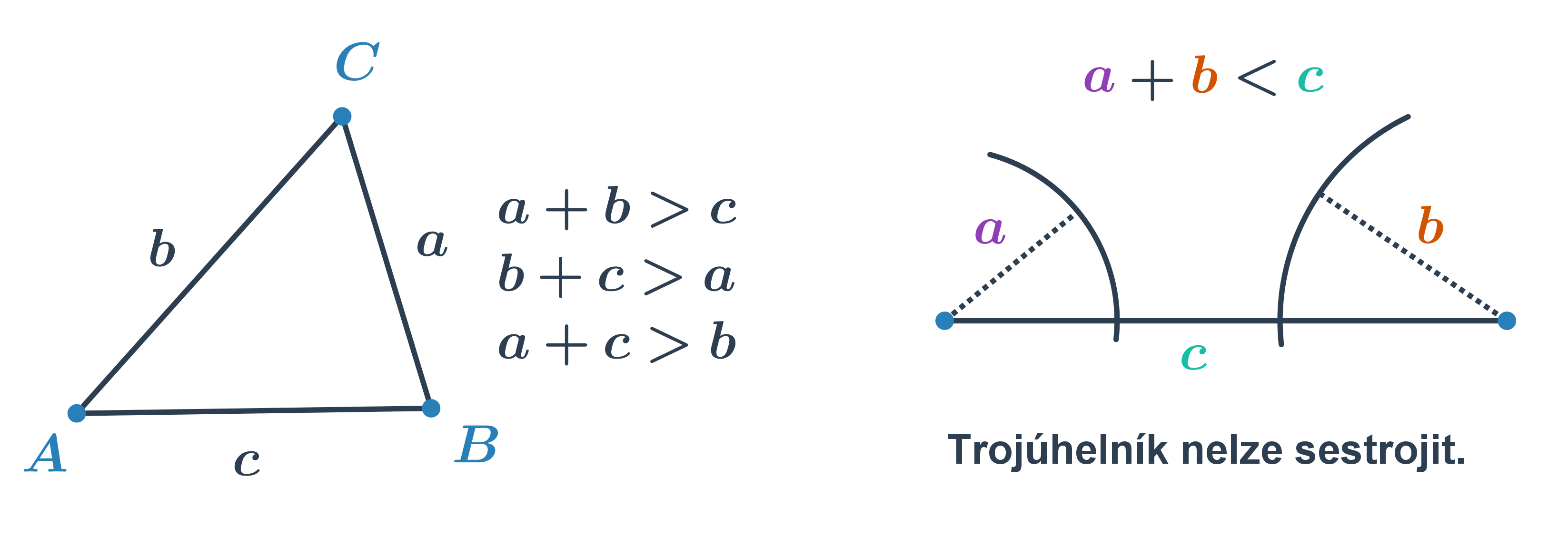
Občas má některý trojúhelník zajímavou vlastnost, která nám pomůže odvodit si potřebné informace k jeho sestrojení — může jít např. o konstrukci rovnoramenného nebo rovnostranného trojúhelníku.
Při řešení složitějších příkladů provádíme konstrukci trojúhelníků podle vět sss, sus, usu, Ssu, využíváme přitom známé věty o sestrojitelnosti trojúhelníků.
U nejtěžších příkladů, jako je konstrukce trojúhelníků, kdy známé údaje zahrnují těžnice, výšky, opsanou nebo vepsanou kružnici trojúhelníka využíváme při konstrukci další pojmy související s trojúhelníkem, či množiny bodů daných vlastností.
Konstrukce trojúhelníků: známé délky stran
Při konstrukci trojúhelníků můžeme každou stranu označit dvěma způsoby:
- přímo – strana a
- pomocí vrcholů – strana AB
Při konstrukcích trojúhelníků, u kterých známe tři strany, postupujeme tak, že sestrojíme jako první libovolnou stranu, na obrázku například AB. K nalezení posledního vrcholu C použijeme dvě kružnice nebo jejich části. Výsledkem konstrukce jsou dva shodné (stejné) trojúhelníky, proto stačí sestrojit jen jeden.
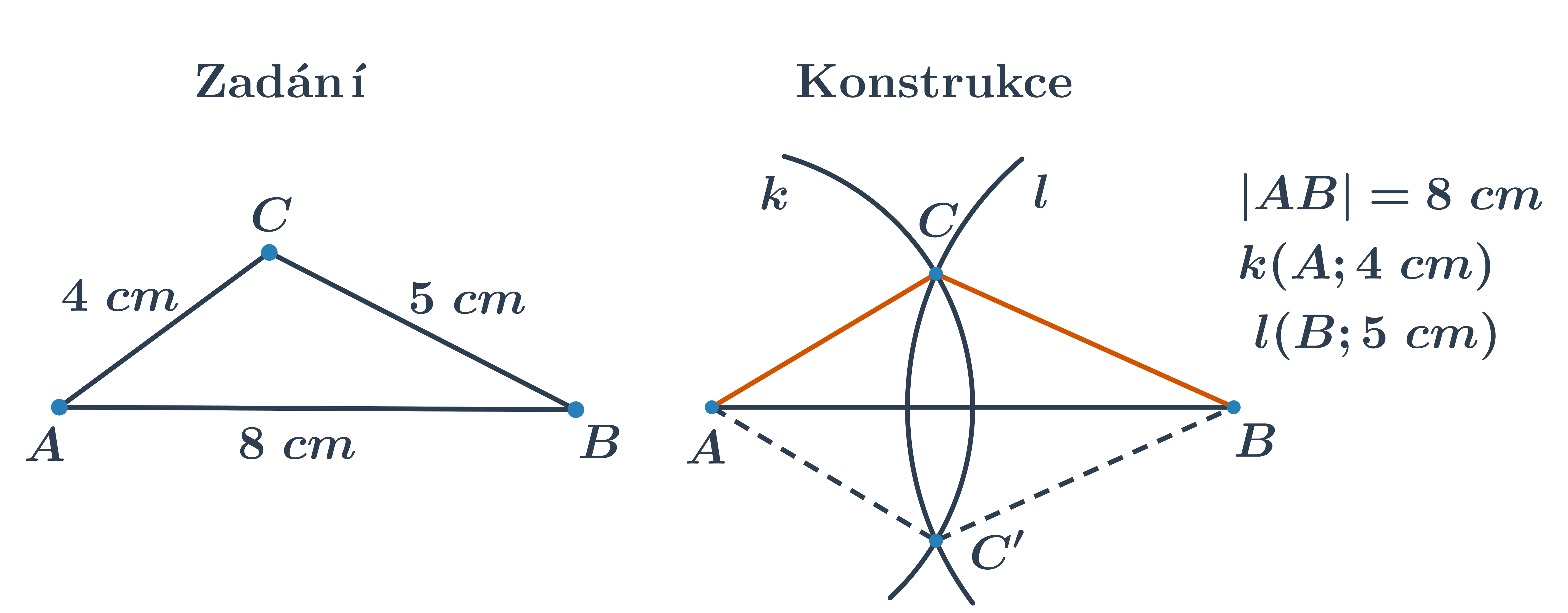
Konstrukce trojúhelníků: rovnoramenné a rovnostranné trojúhelníky
Při konstrukci rovnoramenného trojúhelníku využíváme jeho základní vlastnosti:
- Má dvě strany (ramena) shodné. Vrchol proti základně tedy leží na ose základny.
- Shodné (stejně velké) jsou i vnitřní úhly při základně.
- Výška kolmá na základnu leží na ose základny a dělí rovnoramenný trojúhelník na dva shodné trojúhelníky.
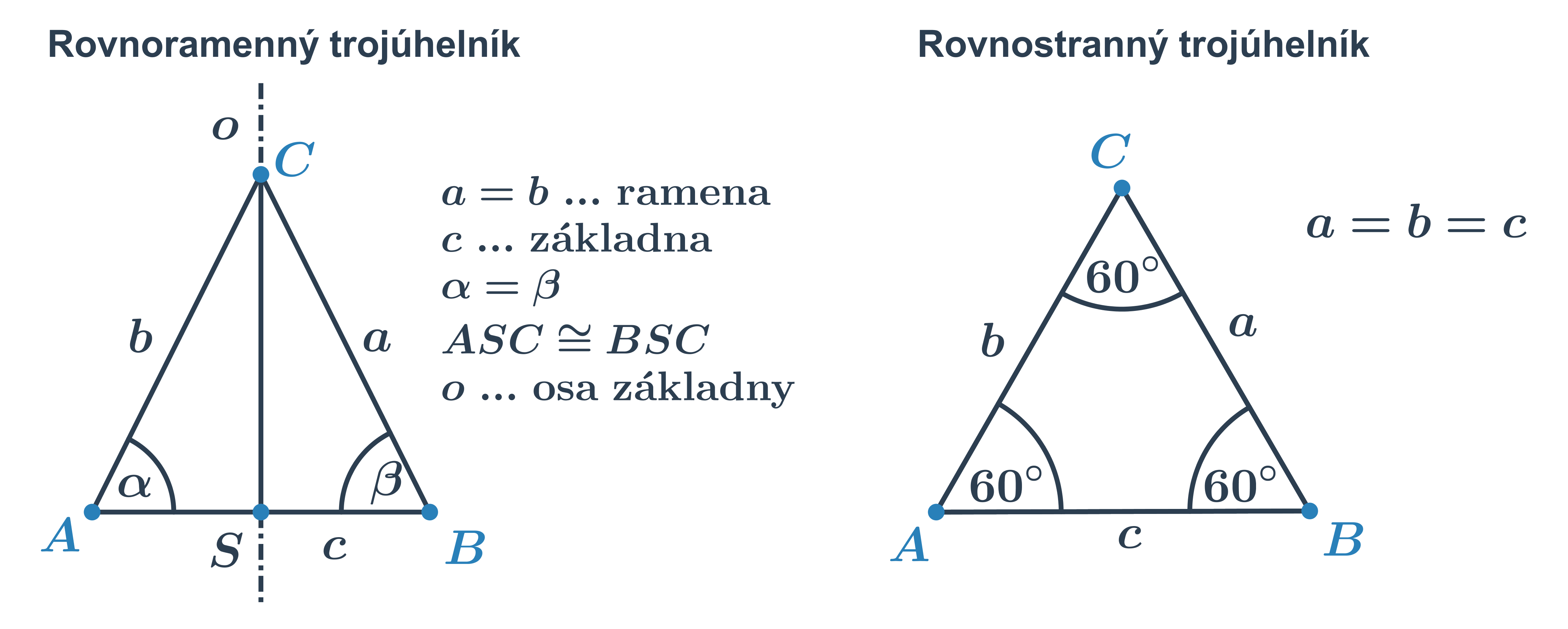
Rovnostranný trojúhelník můžeme chápat jako speciální případ rovnoramenného trojúhelníka. Má všechny strany stejně dlouhé a velikost všech jeho vnitřních úhlů je 60°.
Konstrukce trojúhelníků: věty sss, sus, usu, Ssu
Při složitějších příkladech využíváme věty o sestrojitelnosti trojúhelníků (kde s značí stranu a u úhel)
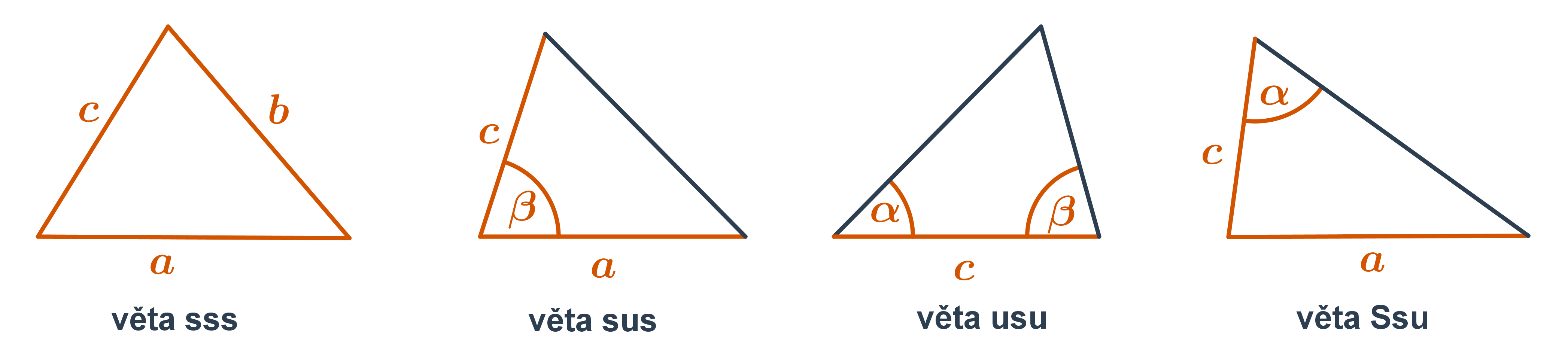
- věta sss - v trojúhelníku jsou dány délky všech stran, pro které platí trojúhelníková nerovnost.
- Věta sus - v trojúhelníku jsou dány délky dvou stran a velikost úhlu, který svírají (menší než 180°).
- Věta usu - v trojúhelníku je dána délka jedné strany a velikosti 2 úhly k ní přiléhající (součet velikostí daných úhlů je menší než 180°).
- Věta ssu - známe velikosti dvou stran trojúhelníka a velikost úhlu proti větší z těchto stran (velikost zadaného úhlu je menší než 180°).
Konstrukce trojúhelníků: těžnice, výšky, vepsaná a opsaná kružnice
Při řešení složitějších příkladů použijeme další pojmy související s trojúhelníkem, například výška, těžnice, střední příčka, kružnice opsaná či vepsaná.
Těžnice je úsečka, která spojuje vrchol trojúhelníku se středem protější strany. Každý trojúhelník má tři těžnice a jejich průsečík tvoří těžiště trojúhelníku. Těžiště rozděluje každou těžnici v poměru 2 : 1. Delší část těžnice je úsečka mezi vrcholem a těžištěm.
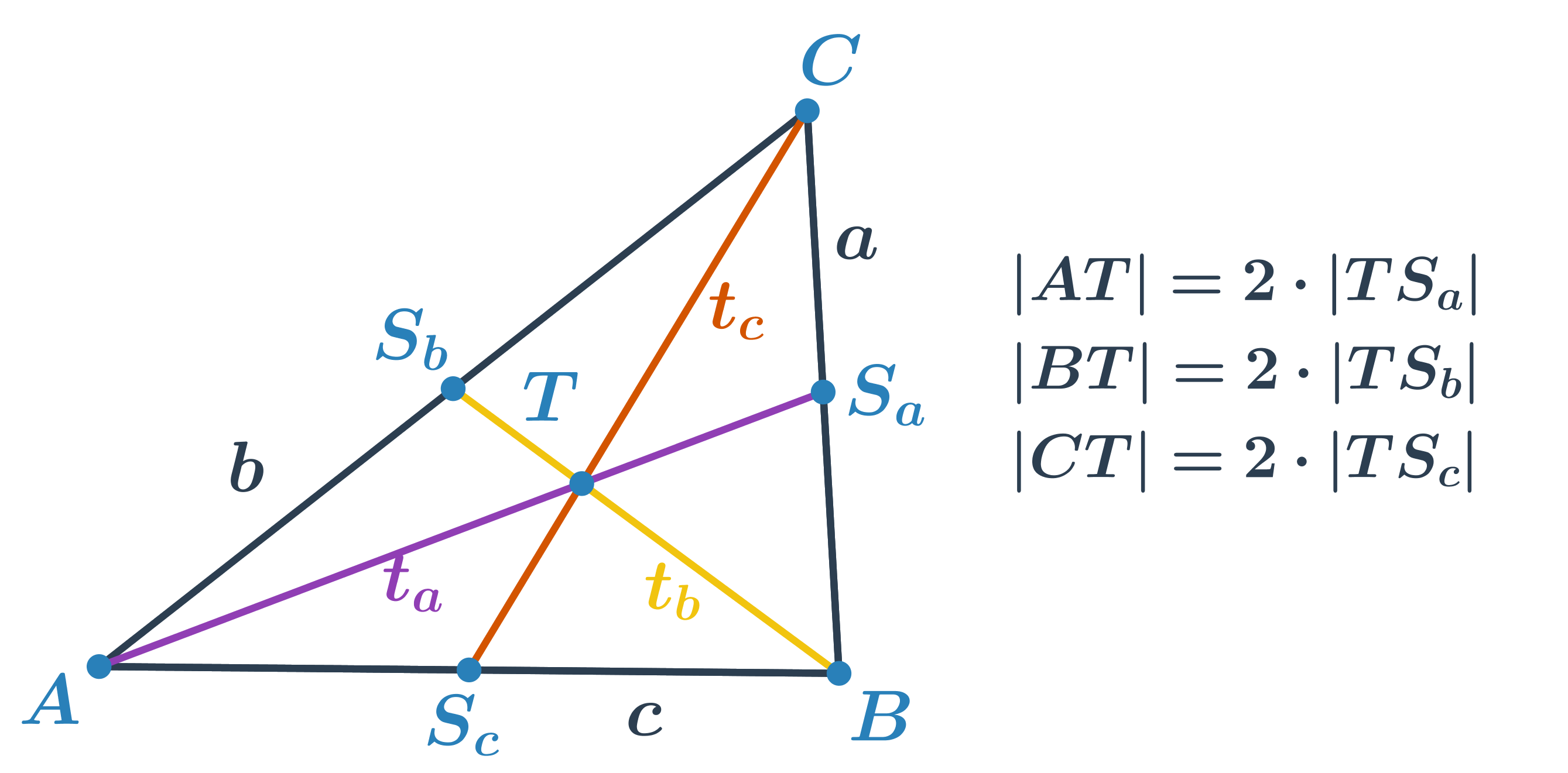
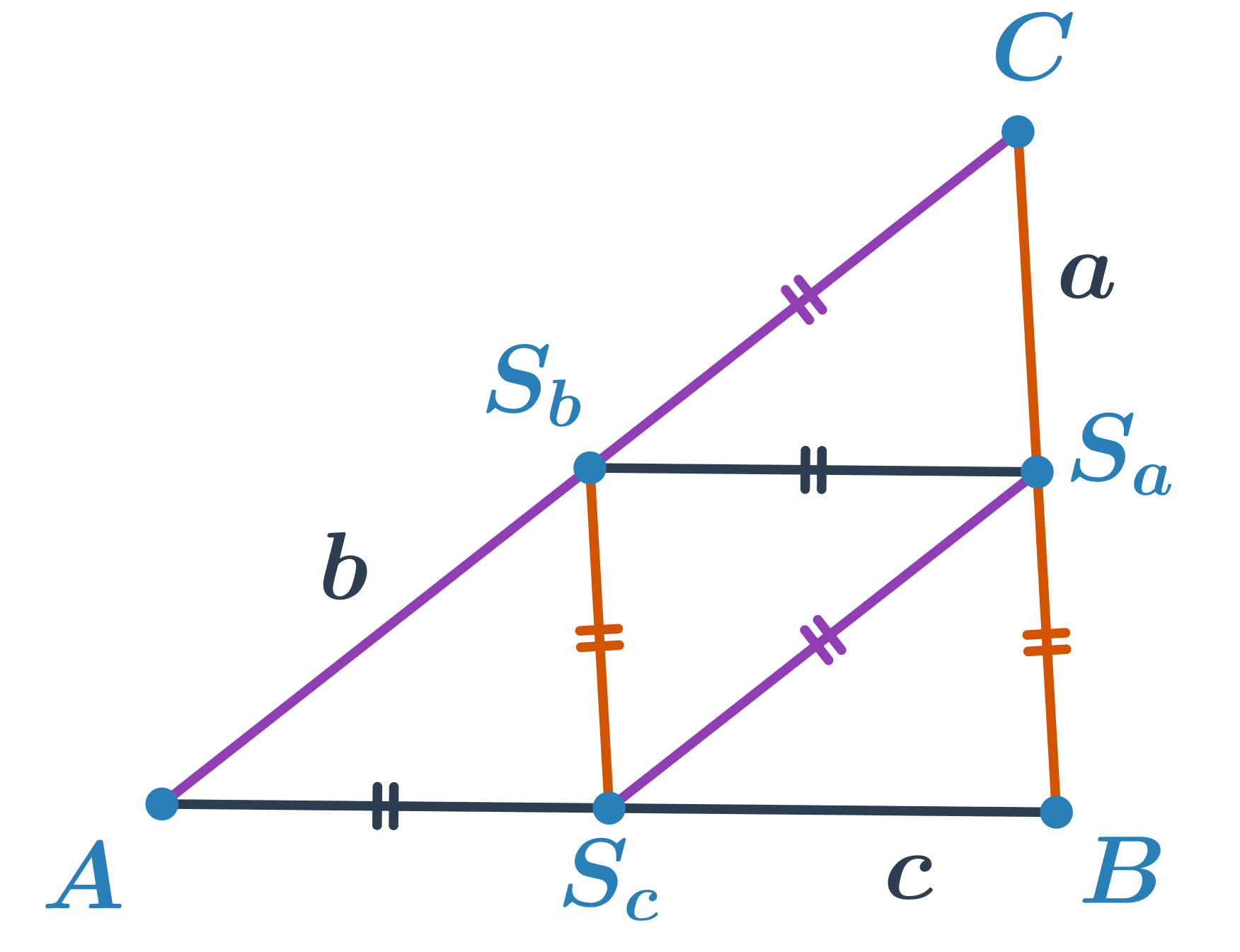
Střední příčka trojúhelníku je úsečka, která spojuje středy 2 stran v trojúhelníku. Je rovnoběžná se stranou, jejíž střed nespojuje a její délka je rovna polovině délky této strany.
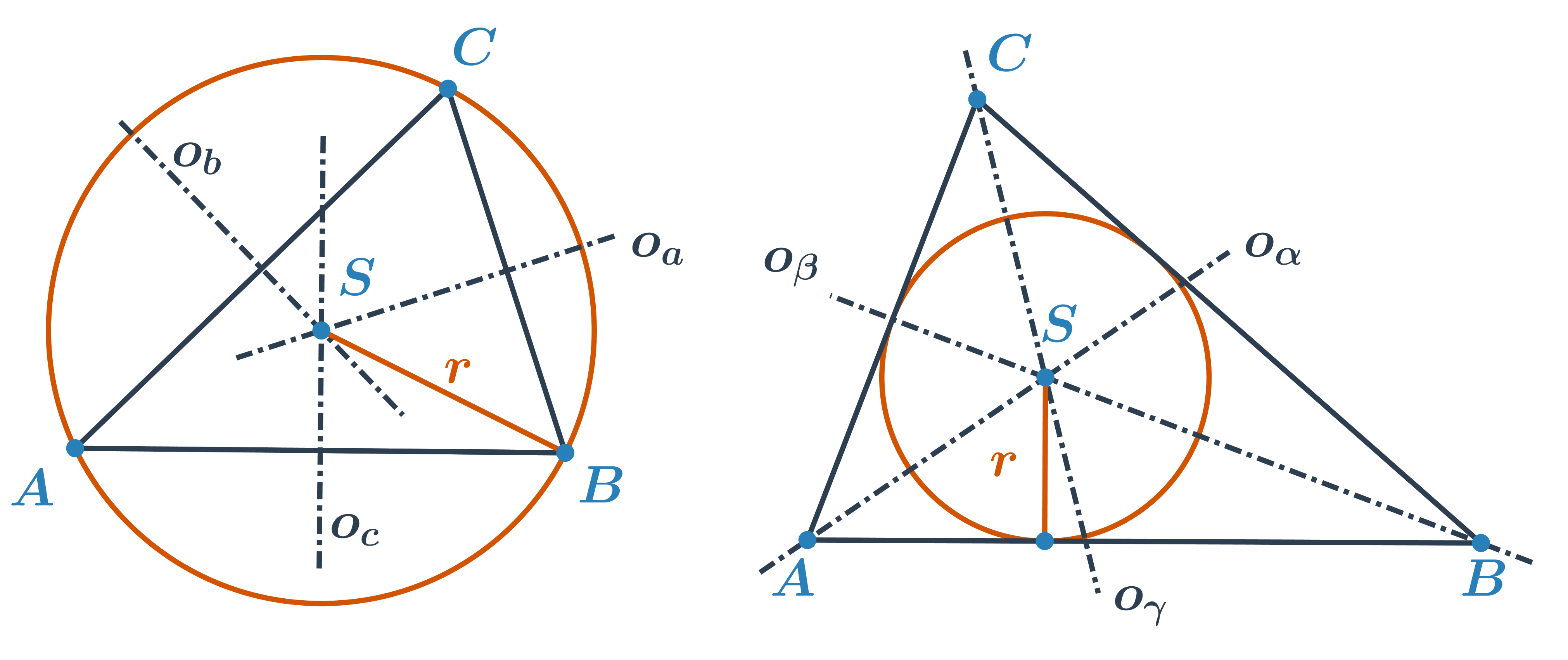
Kružnice opsaná je kružnice, která prochází všemi vrcholy trojúhelníka. Její střed leží v průsečíku os stran. To znamená, že střed kružnice opsané je stejně vzdálen od všech vrcholů trojúhelníku.
Kružnice vepsaná je kružnice, která se dotýká všech stran trojúhelníku. Její střed leží v průsečíku os vnitřních úhlů trojúhelníku. To znamená, že střed kružnice vepsané je stejně vzdálen od všech tří přímek, na kterých leží strany trojúhelníku.
Konstrukční úlohy průřezově
Při řešení složitějších konstrukčních úloh budeme využívat i množiny bodů daných vlastností. Připomeňme si ty nejdůležitější.
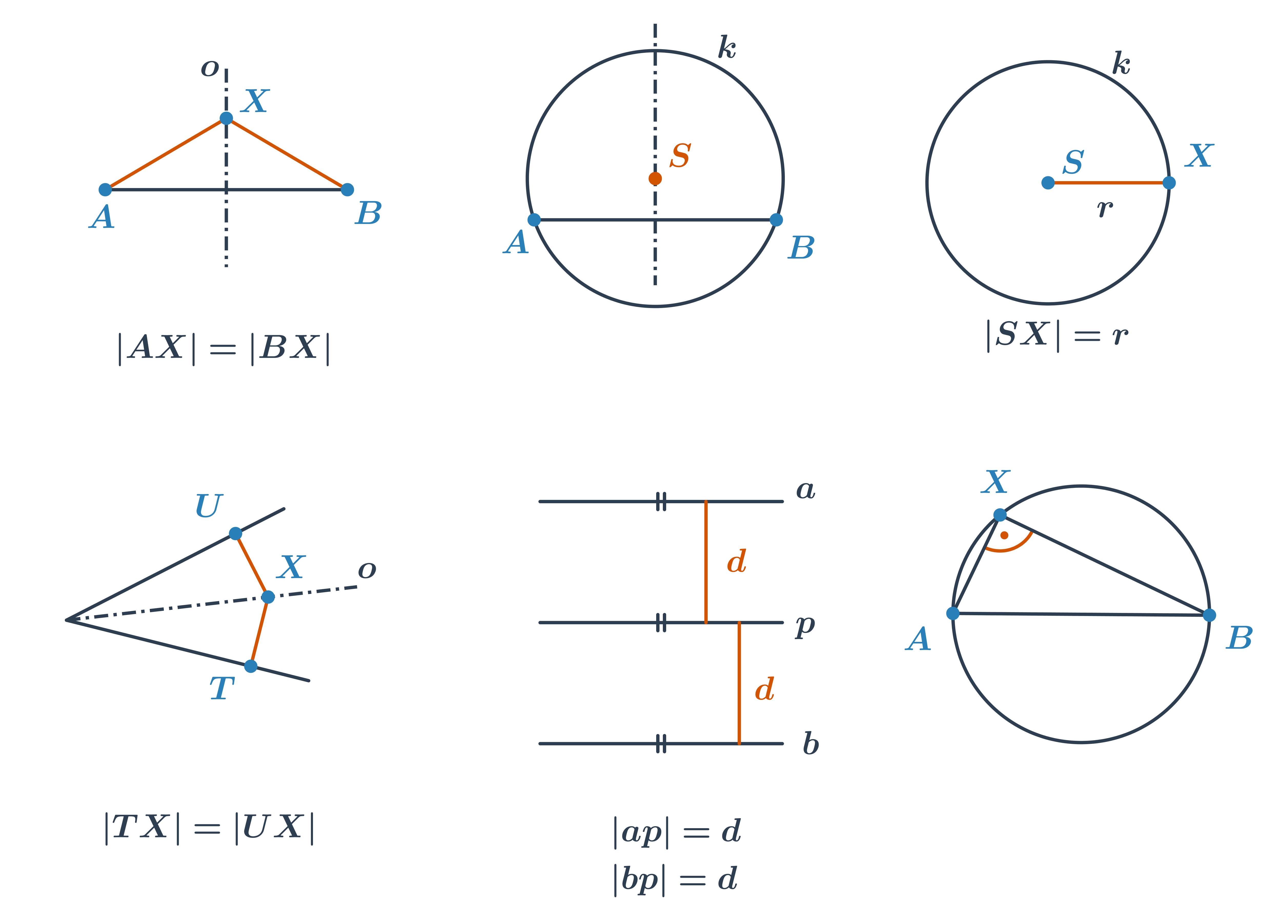
| Osa úsečky AB | množina všech bodů, které mají od bodů A, B stejnou vzdálenost |
| Osa úsečky AB | množina středů všech kružnic, které prochází body A, B |
| Kružnice | množina všech bodů, které mají od bodu S stejnou vzdálenost (poloměr r) |
| Osa úhlů | množina všech bodů, které mají od ramen úhlu stejnou vzdálenost |
| Rovnoběžky | množiny všech bodů, které mají od přímky p stejnou vzdálenost |
| Thaletova kružnice nad úsečkou AB | množina všech vrcholů pravých úhlů, jejichž ramena procházejí body A, B |