Zpět na hlavní stránku

Shodnost a podobnost

---

Podobnost

Podobnost je geometrické zobrazení Euklidovského prostoru do sebe, které násobí všechny vzdálenosti stejným koeficientem, tzv. měřítkem podobnosti. Dva geometrické útvary v Euklidově prostoru jsou podobné , pokud oba mají přesně stejný tvar. Přesněji řečeno, jeden je shodný s útvarem, získaným jako výsledek rovnoměrného zmenšení či zvětšení druhého a jeho případné rotace, posunutí a zrcadlení. Nejjednodušším příkladem podobného zobrazení je stejnolehlost. Podobnost je speciálním případem afinity. Speciálním případem podobnosti, je-li koeficient podobnosti roven 1, je shodnost.

Poměr vzdálenosti dvou bodů daného geometrického útvaru a vzdálenosti odpovídajících dvou bodů jiného geometrického útvaru (referenčního) je u podobných útvarů shodný pro každou takovou dvojici bodů a nazývá se koeficient podobnosti. Podobnost zachovává velikost úhlů a poměr délek.

Podobnost v rovině

Pro rovinné útvary z toho vyplývá, že odpovídající hrany podobných mnohoúhelníků jsou ve vzájemném poměru a odpovídající úhly si jsou rovny.

Například všechny kružnice, čtverce a rovnostranné trojúhelníky si jsou podobné. Naopak elipsy si podobné být nemusí, stejně tak jako hyperboly.

Zpravidla se za speciální případ podobnosti považuje i shodnost, tedy podobnost s koeficientem podobnosti k = 1. Zpravidla se za speciální případ podobnosti považuje i shodnost, tedy podobnost s koeficientem podobnosti

Podobné trojúhelníky

Trojúhelníky △ABC a △DEF jsou podobné (píšeme △ABC ~ △DEF), pokud vyhoví jedné z následujících vět:

1. Věta sss – Každé dva trojúhelníky, které mají sobě rovné poměry délek všech tří dvojic odpovídajících stran, jsou si podobné.
• odpovídající strany mají délky ve stejném poměru, takže platí $\frac{{\mathrm{AB}}_{}}{{\mathrm{DE}}_{}}$ = $\frac{{\mathrm{BC}}_{}}{{\mathrm{EF}}_{}}$ = $\frac{{\mathrm{AC}}_{}}{{\mathrm{DF}}_{}}$ = k a trojúhelníky jsou si podobné.
2. Věta sus – Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu jimi sevřeném, jsou si podobné.
3. Věta uu – Každé dva trojúhelníky, které mají dva úhly stejné, jsou si podobné.
• je-li úhel ∠BAC roven ∠EDF a ∠ABC je roven ∠DEF, pak to znamená, že i ∠ACB je roven ∠DFE a trojúhelníky jsou si podobné.
4. Věta Ssu – Každé dva trojúhelníky, které mají sobě rovné poměry délek dvou odpovídajících stran a shodují se v úhlu naproti větší straně, jsou si podobné.

Podobné trojúhelníky jsou tedy takové, které mají stejný tvar, ale jinou velikost (tvar trojúhelníku je definován jeho úhly). Je to možné říci i tak, že jeden trojúhelník je zvětšením (či zmenšením) druhého.

Podobné mnohoúhelníky

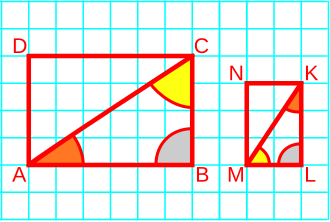
Tuto myšlenku je možné rozšířit na mnohoúhelníky s více stranami. U jakýchkoli dvou podobných mnohoúhelníků si jsou odpovídající strany přímo úměrné. Nicméně pouze úměrnost stran není dostatečná k zajištění podobnosti mnohoúhelníků kromě trojúhelníků, takže odpovídající úhly rovněž musí být shodné.

Shodné zobrazení (shodnost)

Shodné zobrazení je v geometrii takové zobrazení mezi Euklidovskými prostory, které zachovává vzdálenost.

Shodné zobrazení prostoru do sebe se nazývá shodnost.

V elementární školské geometrii se studují shodnosti v rovině a (trojrozměrném) prostoru.

Obecně se pro metrické prostory zavádí pojem izometrické zobrazení (izometrie).

Základní vlastnosti

• Složením shodných zobrazení vznikne opět shodné zobrazení.
• Shodné zobrazení je prosté.
• Pro každé shodné zobrazení je inverzní zobrazení opět shodné.
• Identita je shodné zobrazení.
• Všechny shodnosti euklidovského prostoru tvoří s operací skládání zobrazení grupu shodností, tzv. euklidovskou grupu.

Shodnosti v rovině

Druhy shodností

V rovině existují jenom následující druhy shodností:

• posunutí (translace) - všechny body roviny jsou posunuty stejným směrem o stejnou vzdálenost - směr a vzdálenost jsou dány orientovanou úsečkou nebo vektorem posunutí.
• otočení (rotace) - všechny body roviny jsou otočeny kolem pevně daného bodu (středu otočení) stejným směrem o stejný úhel (úhel otočení)
• středová souměrnost (středová symetrie) - středová souměrnost v rovině je zvláštní případ otočení - otočení kolem středu souměrnosti o 180 stupňů
• osová souměrnost (zrcadlení, osová symetrie) - pro danou pevnou přímku (osu souměrnosti) platí, že na ní leží střed spojnice vzoru a obrazu.
• posunutá (osová) souměrnost - složení osové souměrnosti a posunutí ve směru osy.
• totožnost (identita) - zobrazení, které každý bod zobrazuje na sebe sama. Lze ji považovat za posunutí o úsečku nulové délky nebo za otočení o nulový úhel.

Skládání shodností

• Složením (dvou) posunutí je opět posunutí.
• Složením dvou středových souměrností je posunutí.
• Složením dvou otočení se stejným středem je opět otočení se stejným středem.
• Složením dvou osových souměrností se stejnou osou je identita.
• Složením dvou osových souměrností s různými rovnoběžnými osami je posunutí. Každé posunutí lze vyjádřit jako složení dvou osových souměrností.
• Složením dvou osových souměrností s různoběžnými osami je otočení kolem průsečíku os. Každé otočení lze vyjádřit jako složení dvou osových souměrností.
• Inverzní zobrazení ke shodnému zobrazení je stejného typu, jako původní zobrazení (například inverzním zobrazením k posunutí je opět posunutí).

Každou shodnost v rovině lze složit (různými způsoby) nejvýše ze třiosových souměrností. Obecně každou shodnost v n-rozměrném euklidovském prostoru lze složit nejvýše z (n+1) souměrností podle nadroviny (zrcadlení generují euklidovskou grupu).

Přímá a nepřímá shodnost

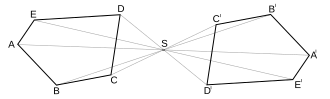
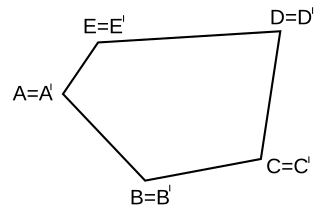
Při pokusech se zobrazením trojúhelníku v různých shodnostech si nelze nevšimnout jedné zajímavé věci - někdy jsou vrcholy obrazu trojúhelníku „pojmenovány“ ve stejném směru (například A,B,C po směru hodinových ručiček se zobrazí na A′,B′,C′ opět po směru hodinových ručiček), někdy naopak (vzor je A,B,C po směru, ale obraz je A′,B′,C′ proti směru). Mluvíme o zachování orientace a o shodném zobrazení zachovávajícím orientaci nebo naopak o změně orientace a o shodném zobrazení měnícím orientaci.

Shodnost zachovávající orientaci se nazývá přímá neboli přemístění. Shodnost měnící orientaci se nazývá nepřímá.

• Posunutí a otočení (a tedy i středová souměrnost) jsou přímé shodnosti (přemístění), zachovávají orientaci.
• (Posunuté) osové souměrnosti jsou nepřímé shodnosti, mění orientaci.

Každé přemístění v rovině lze složit (různými způsoby) ze dvou osových souměrností.

• Složením (dvou) přímých shodností je přímá shodnost.
• Složením přímé a nepřímé shodnosti je nepřímá shodnost.
• Složením dvou nepřímých shodností je přímá shodnost.
• Složením sudého počtu nepřímých shodností je přímá shodnost.
• Složením lichého počtu nepřímých shodností je nepřímá shodnost.

Shodnosti v prostoru

Druhy shodností

V prostoru existují jenom následující druhy shodností:

• posunutí (translace) - všechny body prostoru jsou posunuty stejným směrem o stejnou vzdálenost - směr a vzdálenost jsou dány orientovanou úsečkou nebo vektorem posunutí.
• otočení (rotace) - všechny body roviny jsou otočeny kolem pevně dané přímky (osy otočení, rotační osy) stejným směrem o stejný úhel (úhel otočení)
• rovinová souměrnost (zrcadlení)
• středová souměrnost (prostorová inverze) - na rozdíl od rovinné středové souměrnosti nelze realizovat jako složení 2 rotací
• totožnost (identita) - zobrazení, které každý bod zobrazuje na sebe sama. Lze ji považovat za posunutí o úsečku nulové délky nebo za otočení o nulový úhel.
• a jejich netriviální složení.